from fastbook import *Модель языка с нуля
Теперь мы готовы углубиться ... в глубокое обучение! Вы уже научились обучать базовую нейронную сеть, но как оттуда перейти к созданию современных моделей? В этой части книги мы собираемся раскрыть все загадки, начиная с языковых моделей.
Вы видели в < >, как настроить предварительно обученную языковую модель для создания классификатора текста. В этой главе мы объясним вам, что именно находится внутри этой модели и что такое RNN. Во-первых, давайте соберем некоторые данные, которые позволят нам быстро создать прототипы наших различных моделей.
Данные
Всякий раз, когда мы начинаем работать над новой проблемой, мы всегда сначала пытаемся придумать самый простой набор данных, который мы можем, который позволит нам быстро и легко опробовать методы и интерпретировать результаты. Когда мы начали работать над языковым моделированием несколько лет назад, мы не нашли никаких наборов данных, которые позволяли бы быстро создавать прототипы, поэтому мы их создали. Мы называем это человеческими числами , и он просто содержит первые 10 000 чисел, написанных на английском языке.
Дж .: Одна из наиболее распространенных практических ошибок, которые я вижу даже среди опытных практиков, - это неспособность использовать соответствующие наборы данных в подходящие моменты в процессе анализа. В частности, большинство людей склонны начинать со слишком больших и слишком сложных наборов данных.
Мы можем загрузить, извлечь и просмотреть наш набор данных обычным способом:
from fastai.text.all import *
path = untar_data(URLs.HUMAN_NUMBERS)#hide
Path.BASE_PATH = pathpath.ls()(#2) [Path('valid.txt'),Path('train.txt')]
Давайте откроем эти два файла и посмотрим, что внутри. Сначала мы объединим все тексты вместе и проигнорируем разделение train/valid, указанное в наборе данных (мы вернемся к этому позже):
lines = L()
with open(path/'train.txt') as f: lines += L(*f.readlines())
with open(path/'valid.txt') as f: lines += L(*f.readlines())
lines(#9998) ['one \n','two \n','three \n','four \n','five \n','six \n','seven \n','eight \n','nine \n','ten \n'...]
Мы берем все эти строки и объединяем их в один большой поток. Чтобы отметить, когда мы переходим от одного числа к другому, мы используем . в качестве разделителя:
text = ' . '.join([l.strip() for l in lines])
text[:100]'one . two . three . four . five . six . seven . eight . nine . ten . eleven . twelve . thirteen . fo'
Мы можем токенизировать этот набор данных, разделив его на пробелы:
tokens = text.split(' ')
tokens[:10]['one', '.', 'two', '.', 'three', '.', 'four', '.', 'five', '.']
Чтобы оцифровать, мы должны создать список всех уникальных токенов (наш словарь ):
vocab = L(*tokens).unique()
vocab(#30) ['one','.','two','three','four','five','six','seven','eight','nine'...]
Затем мы можем преобразовать наши токены в числа, просмотрев индекс каждого в словаре:
word2idx = {w:i for i,w in enumerate(vocab)}
nums = L(word2idx[i] for i in tokens)
nums(#63095) [0,1,2,1,3,1,4,1,5,1...]
Теперь, когда у нас есть небольшой набор данных, на котором языковое моделирование должно быть простой задачей, мы можем построить нашу первую модель.
Наша первая языковая модель с нуля
Один простой способ превратить это в нейронную сеть - это указать, что мы собираемся предсказывать каждое слово на основе предыдущих трех слов. Мы могли бы создать список каждой последовательности из трех слов в качестве наших независимых переменных и следующего слова после каждой последовательности в качестве зависимой переменной.
Мы можем сделать это с помощью простого Python. Давайте сначала сделаем это с токенами, чтобы убедиться, как это выглядит:
L((tokens[i:i+3], tokens[i+3]) for i in range(0,len(tokens)-4,3))(#21031) [(['one', '.', 'two'], '.'),(['.', 'three', '.'], 'four'),(['four', '.', 'five'], '.'),(['.', 'six', '.'], 'seven'),(['seven', '.', 'eight'], '.'),(['.', 'nine', '.'], 'ten'),(['ten', '.', 'eleven'], '.'),(['.', 'twelve', '.'], 'thirteen'),(['thirteen', '.', 'fourteen'], '.'),(['.', 'fifteen', '.'], 'sixteen')...]
Теперь мы сделаем это с помощью тензоров числовых значений, которые на самом деле будет использовать модель:
seqs = L((tensor(nums[i:i+3]), nums[i+3]) for i in range(0,len(nums)-4,3))
seqs(#21031) [(tensor([0, 1, 2]), 1),(tensor([1, 3, 1]), 4),(tensor([4, 1, 5]), 1),(tensor([1, 6, 1]), 7), (tensor([7, 1, 8]), 1),(tensor([1, 9, 1]), 10),(tensor([10, 1, 11]), 1),(tensor([ 1, 12, 1]), 13), (tensor([13, 1, 14]), 1),(tensor([ 1, 15, 1]), 16)...]
Мы можем легко объединить их с помощью DataLoader класса. А пока мы разделим последовательности случайным образом:
bs = 64
cut = int(len(seqs) * 0.8)
dls = DataLoaders.from_dsets(seqs[:cut], seqs[cut:], bs=64, shuffle=False)Теперь мы можем создать архитектуру нейронной сети, которая принимает на вход три слова и возвращает прогноз вероятности каждого возможного следующего слова в словаре. Мы будем использовать три стандартных линейных слоя, но с двумя настройками.
Первая настройка заключается в том, что первый линейный уровень будет использовать встраивание только первого слова в качестве активаций, второй уровень будет использовать встраивание второго слова плюс активацию вывода первого уровня, а третий уровень будет использовать вложение третьего слова плюс вывод второго уровня активации. Ключевым эффектом этого является то, что каждое слово интерпретируется в информационном контексте любых предшествующих ему слов.
Вторая настройка заключается в том, что каждый из этих трех слоев будет использовать одну и ту же матрицу весов. То, как одно слово влияет на активацию предыдущих слов, не должно меняться в зависимости от позиции слова. Другими словами, значения активации будут меняться по мере того, как данные перемещаются по слоям, но сами веса слоя не будут меняться от слоя к слою. Итак, слой не узнает одну позицию последовательности; он должен научиться обращаться со всеми позициями.
Поскольку веса слоев не меняются, вы можете думать о последовательных слоях как о повторении одного и того же слоя. Фактически, PyTorch делает этот бетон concrete; мы можем просто создать один слой и использовать его несколько раз.
Наша языковая модель в PyTorch
Теперь мы можем создать модуль языковой модели, который мы описали ранее:
class LMModel1(Module):
def __init__(self, vocab_sz, n_hidden):
self.i_h = nn.Embedding(vocab_sz, n_hidden)
self.h_h = nn.Linear(n_hidden, n_hidden)
self.h_o = nn.Linear(n_hidden,vocab_sz)
def forward(self, x):
h = F.relu(self.h_h(self.i_h(x[:,0])))
h = h + self.i_h(x[:,1])
h = F.relu(self.h_h(h))
h = h + self.i_h(x[:,2])
h = F.relu(self.h_h(h))
return self.h_o(h)Как видите, мы создали три слоя:
- Вложение слой ( i_h для ввода в скрытом )
- Линейный слой для создания активаций для следующего слова ( h_h от скрытого до скрытого )
- Окончательный слой линейного предсказать четвертое слово ( h_o для скрытого на выход )
Это может быть проще представить в наглядной форме, поэтому давайте определим простое графическое представление основных нейронных сетей. < > показывает, как мы собираемся представить нейронную сеть с одним скрытым слоем.
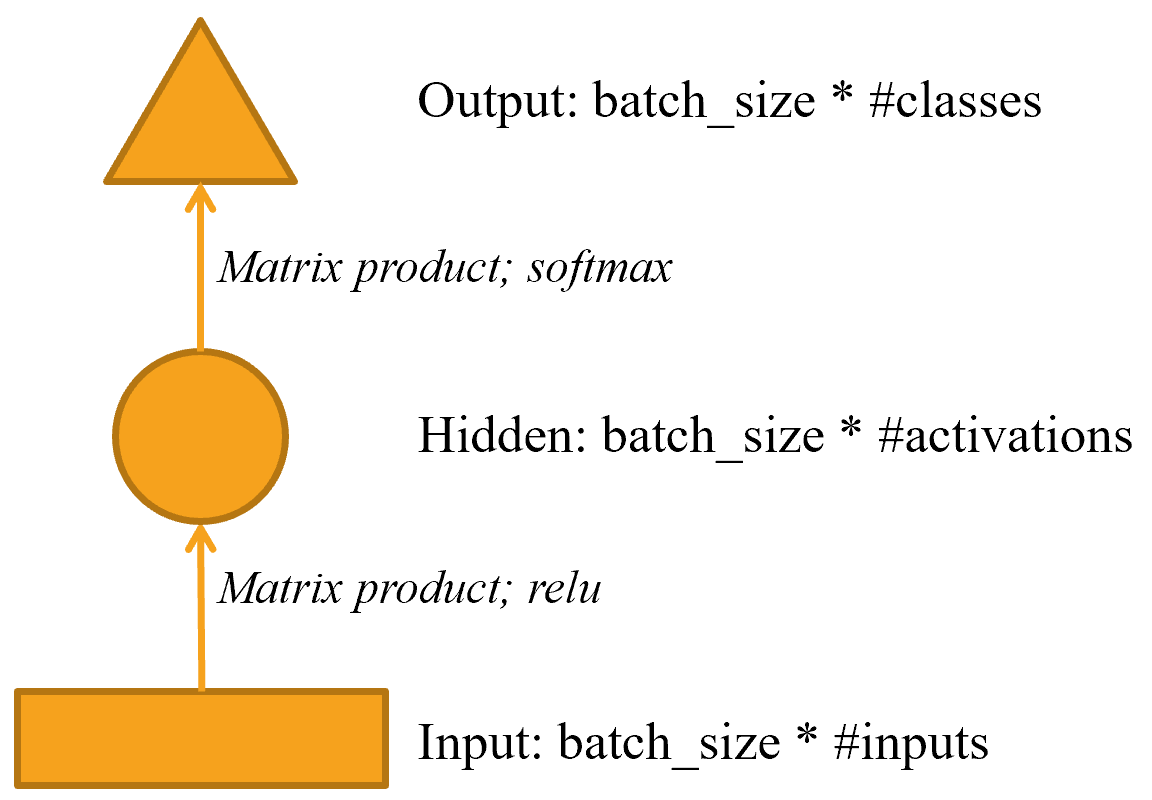
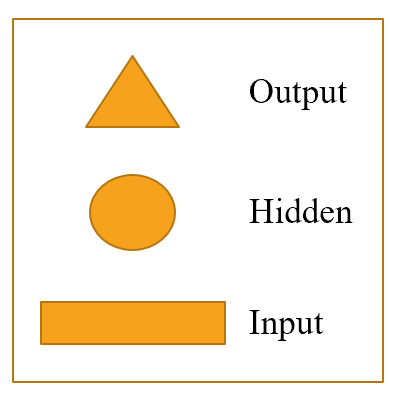
Каждая форма представляет активации: прямоугольник для ввода, круг для активации скрытого (внутреннего) слоя и треугольник для активации вывода. Мы будем использовать эти формы (обозначенные в < >) на всех диаграммах в этой главе.
Стрелка представляет фактическое вычисление слоя, т. Е. Линейный слой, за которым следует функция активации. Используя эту нотацию, < > показывает, как выглядит наша простая языковая модель.
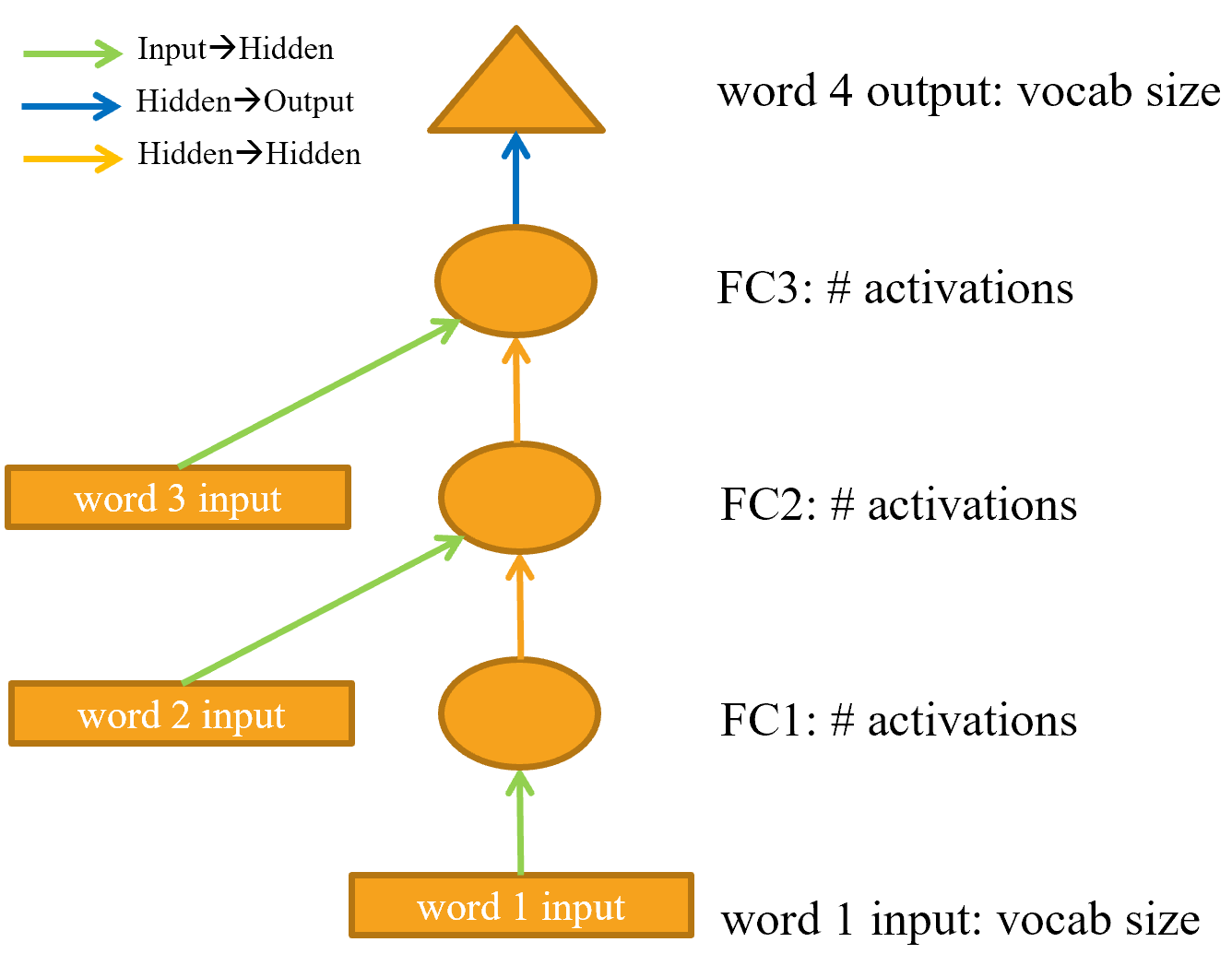
Для упрощения мы удалили детали вычисления слоя с каждой стрелки. Мы также закодировали стрелки по цвету, так что все стрелки одного цвета имеют одинаковую матрицу веса. Например, все входные слои используют одну и ту же матрицу внедрения, поэтому все они имеют одинаковый цвет (зеленый).
Давайте попробуем обучить эту модель и посмотрим, как это работает:
learn = Learner(dls, LMModel1(len(vocab), 64), loss_func=F.cross_entropy,
metrics=accuracy,cbs=ShowGraphCallback())
learn.fit_one_cycle(4, 1e-3)| epoch | train_loss | valid_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 1.834385 | 1.903047 | 0.463751 | 00:01 |
| 1 | 1.403704 | 1.693440 | 0.469693 | 00:01 |
| 2 | 1.409063 | 1.582293 | 0.492750 | 00:01 |
| 3 | 1.371725 | 1.599121 | 0.485382 | 00:01 |
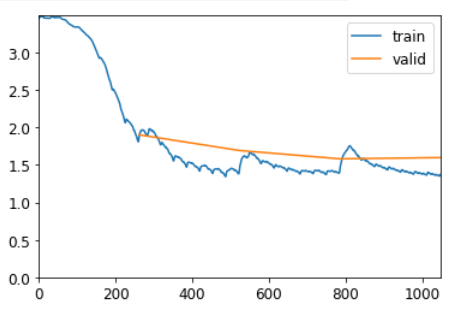
Чтобы увидеть, насколько это хорошо, давайте проверим, что может дать нам очень простая модель. В этом случае мы всегда можем предсказать наиболее распространенный токен, поэтому давайте выясним, какой токен чаще всего является целью в нашем наборе проверки:
n,counts = 0,torch.zeros(len(vocab))
for x,y in dls.valid:
n += y.shape[0]
for i in range_of(vocab): counts[i] += (y==i).long().sum()
idx = torch.argmax(counts)
idx, vocab[idx.item()], counts[idx].item()/n(tensor(29), 'thousand', 0.15165200855716662)
Самый распространенный токен имеет индекс 29, который соответствует токену thousand. Всегда предсказывая этот токен, мы получаем точность примерно 15%, так что у нас дела идут лучше!
A: Я сначала предположил, что разделитель будет наиболее распространенным токеном, поскольку для каждого числа есть один. Но просмотр tokensнапомнил мне, что большие числа пишутся с большим количеством слов, поэтому на пути к 10 000 вы пишете много «тысяча»: пять тысяч, пять тысяч и один, пять тысяч и два и т. Д. Ой! Глядя на свои данные, можно замечать как тонкие, так и до неприличия очевидные особенности.
Это хорошая первая база. Давайте посмотрим, как мы можем реорганизовать его с помощью цикла.
Наша первая рекуррентная нейронная сеть
Глядя на код нашего модуля, мы могли бы упростить его, заменив дублированный код, вызывающий слои, на for цикл. Это не только упрощает наш код, но и имеет то преимущество, что мы сможем одинаково хорошо применять наш модуль к последовательностям токенов разной длины - мы не будем ограничиваться списками токенов длиной три:
class LMModel2(Module):
def __init__(self, vocab_sz, n_hidden):
self.i_h = nn.Embedding(vocab_sz, n_hidden)
self.h_h = nn.Linear(n_hidden, n_hidden)
self.h_o = nn.Linear(n_hidden,vocab_sz)
def forward(self, x):
h = 0
for i in range(3):
h = h + self.i_h(x[:,i])
h = F.relu(self.h_h(h))
return self.h_o(h)Давайте проверим, что мы получили те же результаты, используя этот рефакторинг:
learn = Learner(dls, LMModel2(len(vocab), 64), loss_func=F.cross_entropy,
metrics=accuracy,cbs=ShowGraphCallback())
learn.fit_one_cycle(10, 1e-3)| epoch | train_loss | valid_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 3.027756 | 2.862609 | 0.296886 | 00:01 |
| 1 | 1.537066 | 1.822463 | 0.466603 | 00:01 |
| 2 | 1.376848 | 1.695163 | 0.475636 | 00:01 |
| 3 | 1.326347 | 1.626283 | 0.503684 | 00:01 |
| 4 | 1.284331 | 1.620148 | 0.505586 | 00:01 |
| 5 | 1.273480 | 1.621557 | 0.505586 | 00:01 |
| 6 | 1.264697 | 1.613547 | 0.506299 | 00:01 |
| 7 | 1.262722 | 1.625998 | 0.506774 | 00:01 |
| 8 | 1.250815 | 1.653528 | 0.429047 | 00:01 |
| 9 | 1.242197 | 1.663458 | 0.373663 | 00:01 |
Мы также можем реорганизовать наше графическое представление точно таким же образом, как показано в < > (мы также удаляем детали размеров активации здесь и используем те же цвета стрелок, что и в < >).
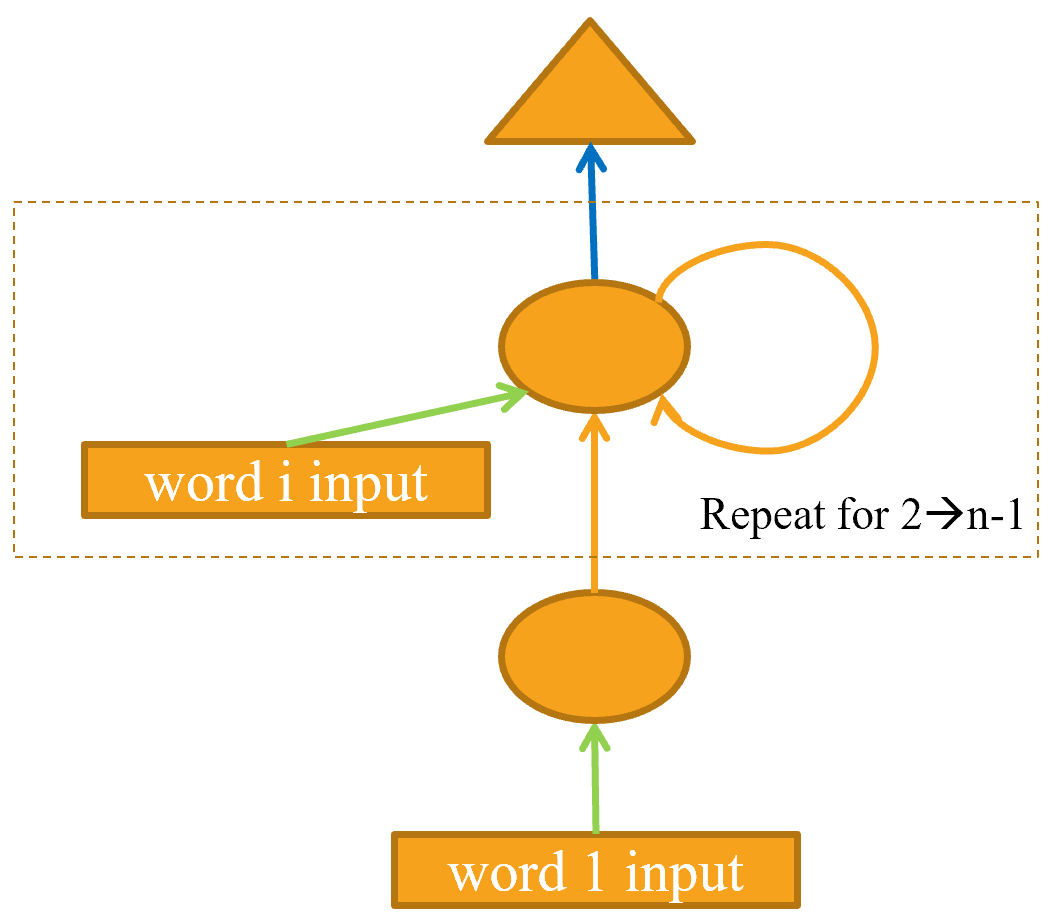
Вы увидите, что существует набор активаций, которые обновляются каждый раз в цикле и хранятся в переменной h- это называется скрытым состоянием
Жаргон: скрытое состояние: активации, которые обновляются на каждом этапе повторяющейся нейронной сети.
Нейронная сеть, которая определяется с помощью такого цикла, называется рекуррентной нейронной сетью (RNN). Важно понимать, что RNN - это не новая сложная архитектура, а просто рефакторинг многослойной нейронной сети с использованием for цикла.
A: Мое истинное мнение: если бы их назвали «петлевыми нейронными сетями» или LNN, они бы казались на 50% менее устрашающими!
Теперь, когда мы знаем, что такое RNN, давайте попробуем сделать его немного лучше.
Улучшение RNN (рекуррентная нейронная сеть)
Глядя на код для нашей RNN, одна вещь, которая кажется проблематичной, заключается в том, что мы инициализируем наше скрытое состояние до нуля для каждой новой входной последовательности. Почему это проблема? Мы сделали наши образцы последовательностей короткими, чтобы их можно было легко объединить в партии. Но если мы упорядочим образцы правильно, эти последовательности образцов будут считываться моделью по порядку, подвергая модель длительным участкам исходной последовательности.
Еще одна вещь, на которую мы можем обратить внимание, - это наличие большего сигнала: зачем предсказывать только четвертое слово, если мы могли бы использовать промежуточные предсказания, чтобы также предсказывать второе и третье слова?
Давайте посмотрим, как мы можем реализовать эти изменения, начиная с добавления некоторого состояния.
Поддержание состояния RNN
Поскольку мы инициализируем скрытое состояние модели равным нулю для каждого нового образца, мы отбрасываем всю имеющуюся у нас информацию о предложениях, которые мы видели до сих пор, а это означает, что наша модель на самом деле не знает, где мы находимся в целом. последовательность подсчета. Это легко исправить; мы можем просто переместить инициализацию скрытого состояния в __init__.
Но это исправление создаст свою тонкую, но важную проблему. Это фактически делает нашу нейронную сеть такой же глубокой, как и все количество токенов в нашем документе. Например, если бы в нашем наборе данных было 10 000 токенов, мы бы создали нейронную сеть с 10 000 уровнями.
Чтобы понять, почему это так, рассмотрим исходное графическое представление нашей рекуррентной нейронной сети в < > перед его рефакторингом с помощью for цикла. Вы можете видеть, что каждый уровень соответствует одному входному токену. Когда мы говорим о представлении рекуррентной нейронной сети до рефакторинга с помощью for цикла, мы называем это развернутым представлением . Часто бывает полезно рассмотреть развернутое представление при попытке понять RNN.
Проблема с нейронной сетью с 10 000 слоями заключается в том, что если и когда вы дойдете до 10 000-го слова набора данных, вам все равно придется вычислять производные вплоть до первого уровня. Это действительно будет очень медленно и потребует очень много памяти. Маловероятно, что вы сможете сохранить на своем графическом процессоре хотя бы одну мини-партию.
Решение этой проблемы - сообщить PyTorch, что мы не хотим распространять производные обратно по всей неявной нейронной сети. Вместо этого мы просто сохраним последние три слоя градиентов. Чтобы удалить всю историю градиентов в PyTorch, мы используем detach метод.
Вот новая версия нашей RNN. Теперь он сохраняет состояние, потому что он запоминает свои активации между различными вызовами forward, которые представляют его использование для разных образцов в пакете:
class LMModel3(Module):
def __init__(self, vocab_sz, n_hidden):
self.i_h = nn.Embedding(vocab_sz, n_hidden)
self.h_h = nn.Linear(n_hidden, n_hidden)
self.h_o = nn.Linear(n_hidden,vocab_sz)
self.h = 0
def forward(self, x):
for i in range(3):
self.h = self.h + self.i_h(x[:,i])
self.h = F.relu(self.h_h(self.h))
out = self.h_o(self.h)
self.h = self.h.detach()
return out
def reset(self): self.h = 0Эта модель будет иметь одинаковые активации независимо от длины последовательности, которую мы выберем, потому что скрытое состояние запомнит последнюю активацию из предыдущего пакета. Единственное, что будет отличаться, - это градиенты, вычисляемые на каждом шаге: они будут вычисляться только для токенов длины последовательности в прошлом, а не для всего потока. Этот подход называется обратным распространением во времени (BPTT).
жаргон: обратное распространение во времени (BPTT): обработка нейронной сети с эффективным использованием одного слоя на временной шаг (обычно рефакторинг с использованием цикла) как одной большой модели и вычисление градиентов на ней обычным способом. Чтобы избежать нехватки памяти и времени, мы обычно используем усеченный BPTT, который «отделяет» историю шагов вычислений в скрытом состоянии каждые несколько временных шагов.
Для использования LMModel3нам нужно убедиться, что образцы будут видны в определенном порядке. Как мы видели в < >, если первая строка первого пакета - наша, dset[0]то второй пакет должен быть dset[1]первой строкой, чтобы модель видела, как текст течет.
LMDataLoaderделал это для нас в < >. На этот раз мы сделаем это сами.
Для этого мы собираемся переупорядочить наш набор данных. Сначала мы разделяем образцы на m = len(dset) // bsгруппы (это эквивалент разделения всего конкатенированного набора данных, например, на 64 части одинакового размера, поскольку мы используем bs=64 здесь). mдлина каждой из этих частей. Например, если мы используем весь наш набор данных (хотя мы фактически разделим его на train, а не valid через мгновение), это будет:
m = len(seqs)//bs
m,bs,len(seqs)(328, 64, 21031)
Первая партия будет состоять из образцов:
(0, m, 2*m, ..., (bs-1)*m)
вторая партия образцов:
(1, m+1, 2*m+1, ..., (bs-1)*m+1)
и так далее. Таким образом, в каждую эпоху модель будет видеть фрагмент непрерывного текста размером 3*m(поскольку каждый текст имеет размер 3) в каждой строке пакета.
Следующая функция выполняет эту переиндексацию:
def group_chunks(ds, bs):
m = len(ds) // bs
new_ds = L()
for i in range(m): new_ds += L(ds[i + m*j] for j in range(bs))
return new_dsЗатем мы просто передаем drop_last=Trueпри построении нашу, DataLoaders чтобы отбросить последнюю партию, которая не имеет формы bs. Также проходим, shuffle=Falseчтобы тексты читались по порядку:
cut = int(len(seqs) * 0.8)
dls = DataLoaders.from_dsets(
group_chunks(seqs[:cut], bs),
group_chunks(seqs[cut:], bs),
bs=bs, drop_last=True, shuffle=False)Последнее, что мы добавим, - это небольшая настройка цикла обучения с помощью файла Callback. Подробнее об обратных вызовах мы поговорим в < >; этот вызовет reset метод нашей модели в начале каждой эпохи и перед каждой фазой проверки. Поскольку мы реализовали этот метод для обнуления скрытого состояния модели, это гарантирует, что мы начнем с чистого состояния перед чтением этих непрерывных фрагментов текста. Мы также можем начать тренировку немного дольше:
learn = Learner(dls, LMModel3(len(vocab), 64), loss_func=F.cross_entropy,
metrics=accuracy, cbs=[ModelResetter,ShowGraphCallback()])
learn.fit_one_cycle(10, 3e-3)| epoch | train_loss | valid_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 1.656055 | 1.842841 | 0.464183 | 00:01 |
| 1 | 1.256587 | 1.826056 | 0.439423 | 00:01 |
| 2 | 1.098412 | 1.754068 | 0.469471 | 00:01 |
| 3 | 1.009238 | 1.577211 | 0.519712 | 00:01 |
| 4 | 0.961432 | 1.628060 | 0.559615 | 00:01 |
| 5 | 0.899862 | 1.568531 | 0.584615 | 00:01 |
| 6 | 0.872120 | 1.487769 | 0.592548 | 00:01 |
| 7 | 0.794920 | 1.499493 | 0.618029 | 00:01 |
| 8 | 0.755065 | 1.540114 | 0.620673 | 00:01 |
| 9 | 0.742821 | 1.539640 | 0.619471 | 00:01 |
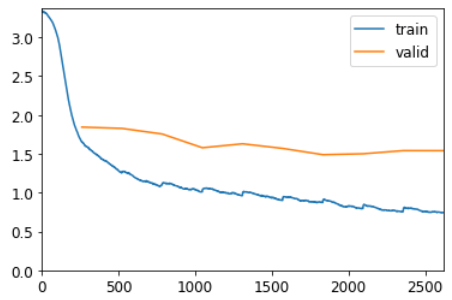
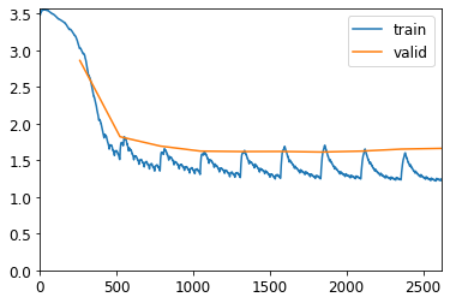
Это уже лучше! Следующий шаг - использовать больше целей и сравнить их с промежуточными прогнозами.
Создание большего сигнала
Другая проблема с нашим текущим подходом заключается в том, что мы прогнозируем только одно выходное слово на каждые три входных слова. Это означает, что количество сигналов, которые мы возвращаем для обновления весов, не так велико, как могло бы быть. Было бы лучше, если бы мы предсказывали следующее слово после каждого слова, а не каждые три слова, как показано в < >.
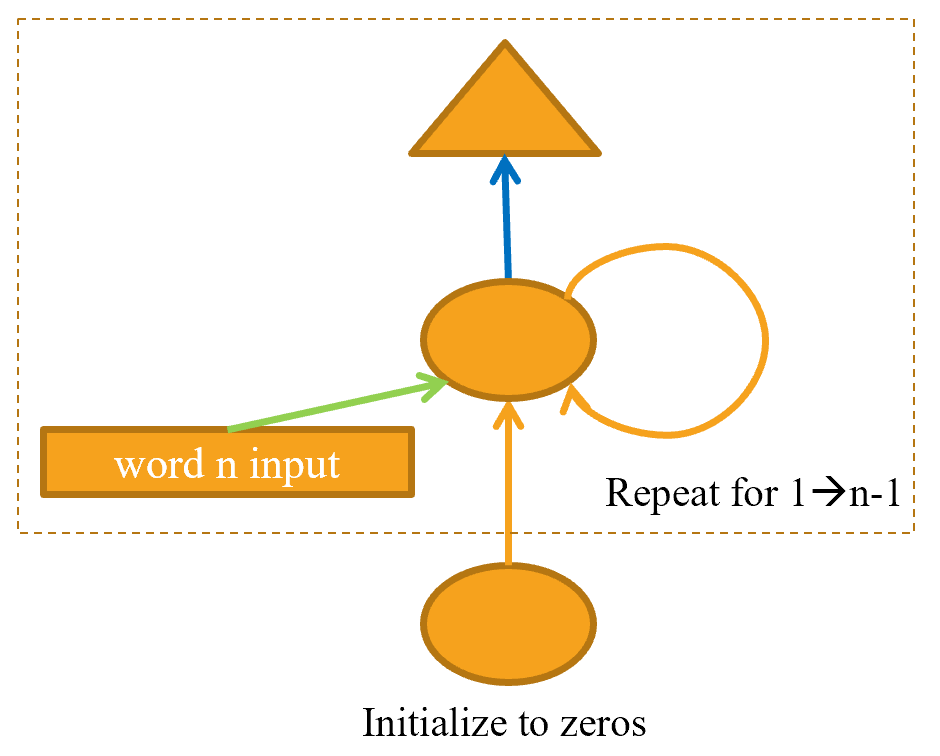
Это достаточно легко добавить. Нам нужно сначала изменить наши данные, чтобы у зависимой переменной было каждое из трех следующих слов после каждого из наших трех входных слов. Вместо этого 3 мы используем атрибут sl(для длины последовательности) и делаем его немного больше:
sl = 16
seqs = L((tensor(nums[i:i+sl]), tensor(nums[i+1:i+sl+1]))
for i in range(0,len(nums)-sl-1,sl))
cut = int(len(seqs) * 0.8)
dls = DataLoaders.from_dsets(group_chunks(seqs[:cut], bs),
group_chunks(seqs[cut:], bs),
bs=bs, drop_last=True, shuffle=False)Глядя на первый элемент seqs, мы видим, что он содержит два списка одинакового размера. Второй список такой же, как и первый, но смещен на один элемент:
[L(vocab[o] for o in s) for s in seqs[0]][(#16) ['one','.','two','.','three','.','four','.','five','.'...], (#16) ['.','two','.','three','.','four','.','five','.','six'...]]
Теперь нам нужно изменить нашу модель, чтобы она выводила предсказание после каждого слова, а не только в конце последовательности из трех слов:
class LMModel4(Module):
def __init__(self, vocab_sz, n_hidden):
self.i_h = nn.Embedding(vocab_sz, n_hidden)
self.h_h = nn.Linear(n_hidden, n_hidden)
self.h_o = nn.Linear(n_hidden,vocab_sz)
self.h = 0
def forward(self, x):
outs = []
for i in range(sl):
self.h = self.h + self.i_h(x[:,i])
self.h = F.relu(self.h_h(self.h))
outs.append(self.h_o(self.h))
self.h = self.h.detach()
return torch.stack(outs, dim=1)
def reset(self): self.h = 0Эта модель будет возвращать результаты формы bs x sl x vocab_sz(так как мы сложили dim=1). Наши цели имеют форму bs x sl, поэтому нам нужно сгладить их, прежде чем использовать в F.cross_entropy:
def loss_func(inp, targ):
return F.cross_entropy(inp.view(-1, len(vocab)), targ.view(-1))Теперь мы можем использовать эту функцию потерь для обучения модели:
learn = Learner(dls, LMModel4(len(vocab), 64), loss_func=loss_func,
metrics=accuracy, cbs=[ModelResetter,ShowGraphCallback()])
learn.fit_one_cycle(15, 3e-3)| epoch | train_loss | valid_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 3.293773 | 3.132215 | 0.192220 | 00:00 |
| 1 | 2.398389 | 2.022170 | 0.461589 | 00:01 |
| 2 | 1.773414 | 1.881746 | 0.465413 | 00:01 |
| 3 | 1.483562 | 1.762913 | 0.488851 | 00:00 |
| 4 | 1.311296 | 1.873363 | 0.512126 | 00:00 |
| 5 | 1.186897 | 1.817782 | 0.533284 | 00:00 |
| 6 | 1.072152 | 1.961689 | 0.552653 | 00:00 |
| 7 | 0.981607 | 1.925002 | 0.574626 | 00:00 |
| 8 | 0.918589 | 2.048767 | 0.570312 | 00:00 |
| 9 | 0.847195 | 2.252135 | 0.586100 | 00:00 |
| 10 | 0.792009 | 2.339236 | 0.603597 | 00:00 |
| 11 | 0.733261 | 2.368746 | 0.607992 | 00:00 |
| 12 | 0.695826 | 2.379836 | 0.608968 | 00:00 |
| 13 | 0.668744 | 2.418024 | 0.605062 | 00:00 |
| 14 | 0.652671 | 2.446920 | 0.606445 | 00:00 |
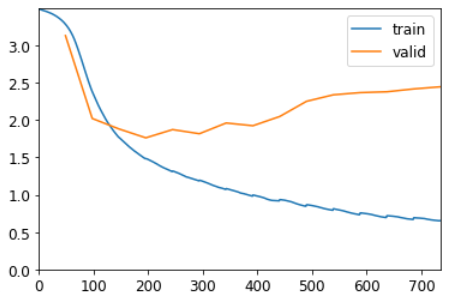
Тренироваться нужно подольше, так как задача немного изменилась и усложнилась. Но в итоге получается хороший результат ... По крайней мере, иногда. Если вы запустите его несколько раз, вы увидите, что можете получить совершенно разные результаты на разных запусках. Это потому, что фактически у нас здесь очень глубокая сеть, которая может приводить к очень большим или очень маленьким градиентам. В следующей части этой главы мы увидим, как с этим справиться.
Теперь очевидный способ получить лучшую модель - это пойти глубже: у нас есть только один линейный слой между скрытым состоянием и активациями вывода в нашей базовой RNN, поэтому, возможно, мы получим лучшие результаты с большим количеством.
Многослойные RNN
В многослойной RNN мы передаем активации из нашей рекуррентной нейронной сети во вторую рекуррентную нейронную сеть, как в < >
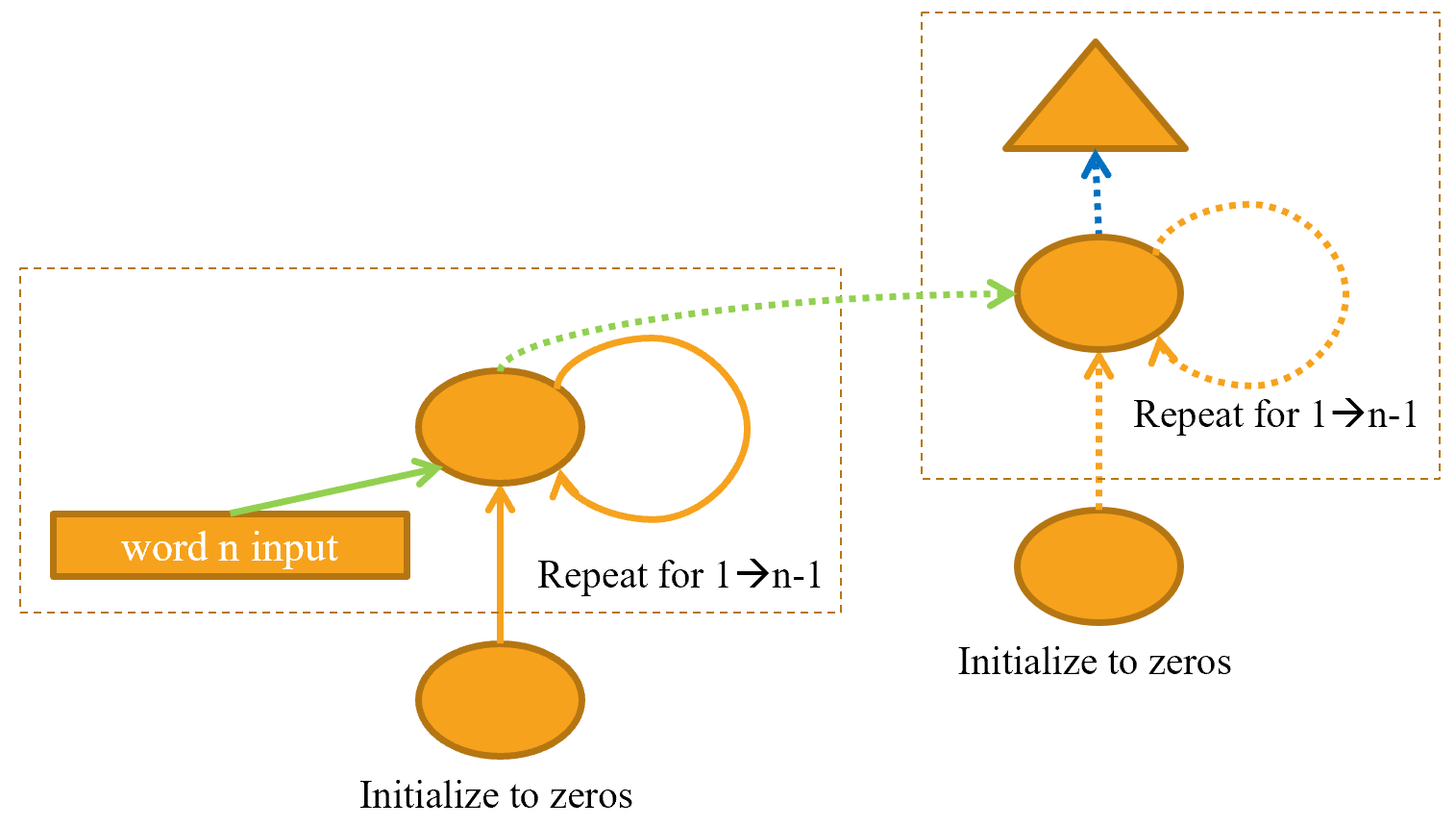
Развернутое представление показано в < > (аналогично < >).
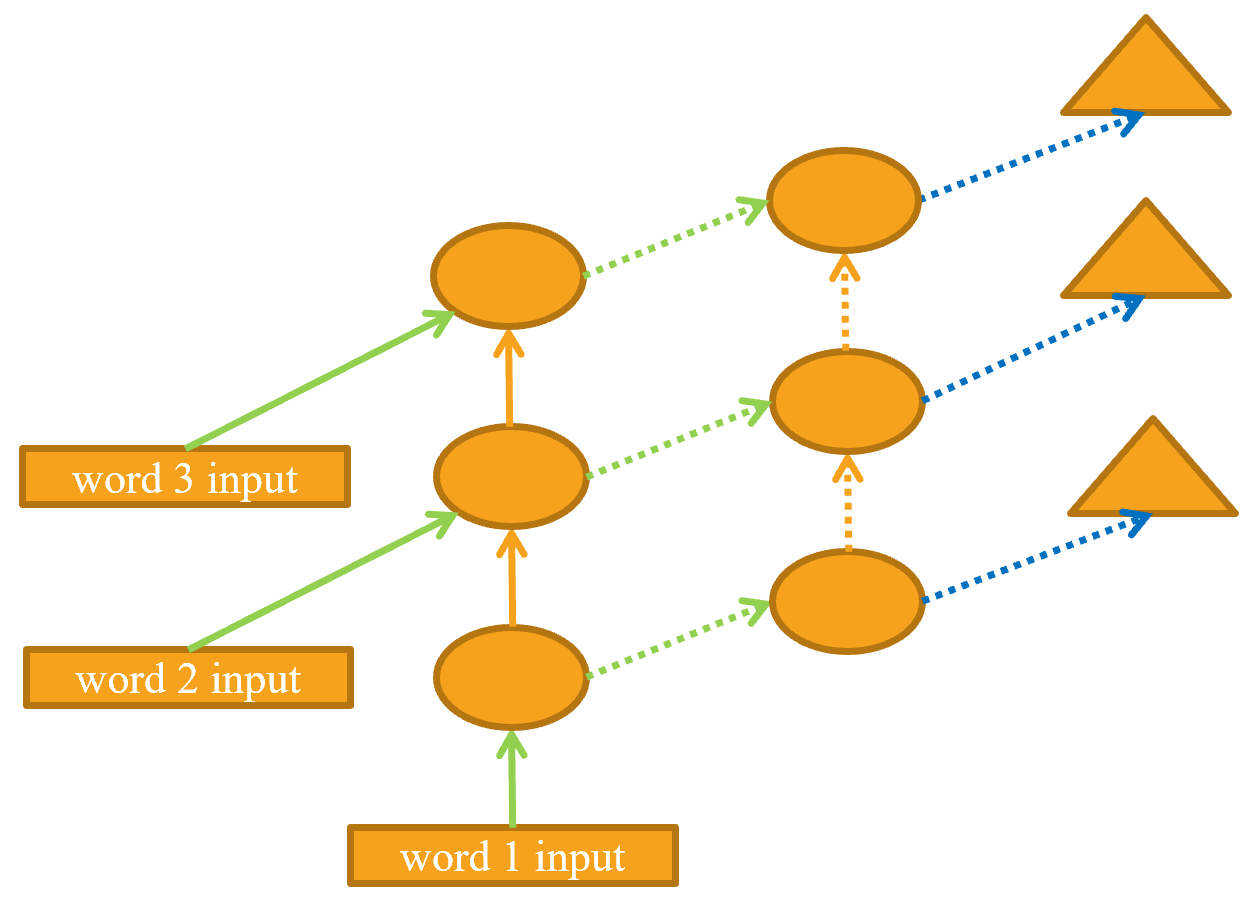
Посмотрим, как это реализовать на практике.
Модель
Мы можем сэкономить время, используя RNNкласс PyTorch , который реализует именно то, что мы создали ранее, но также дает нам возможность складывать несколько RNN, как мы уже обсуждали:
class LMModel5(Module):
def __init__(self, vocab_sz, n_hidden, n_layers):
self.i_h = nn.Embedding(vocab_sz, n_hidden)
self.rnn = nn.RNN(n_hidden, n_hidden, n_layers, batch_first=True)
self.h_o = nn.Linear(n_hidden, vocab_sz)
self.h = torch.zeros(n_layers, bs, n_hidden)
def forward(self, x):
res,h = self.rnn(self.i_h(x), self.h)
self.h = h.detach()
return self.h_o(res)
def reset(self): self.h.zero_()learn = Learner(dls, LMModel5(len(vocab), 64, 2),
loss_func=CrossEntropyLossFlat(),
metrics=accuracy, cbs=[ModelResetter,ShowGraphCallback()])
learn.fit_one_cycle(15, 3e-3)| epoch | train_loss | valid_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 3.060118 | 2.712682 | 0.455322 | 00:01 |
| 1 | 2.164743 | 1.852157 | 0.469808 | 00:01 |
| 2 | 1.709297 | 2.020928 | 0.305827 | 00:00 |
| 3 | 1.493057 | 1.786771 | 0.480550 | 00:00 |
| 4 | 1.327677 | 1.930133 | 0.515788 | 00:00 |
| 5 | 1.162274 | 2.036525 | 0.545003 | 00:00 |
| 6 | 1.022712 | 2.098822 | 0.538330 | 00:01 |
| 7 | 0.891078 | 2.196586 | 0.537354 | 00:01 |
| 8 | 0.757059 | 2.198895 | 0.553223 | 00:00 |
| 9 | 0.653941 | 2.236620 | 0.559163 | 00:01 |
| 10 | 0.581395 | 2.297528 | 0.568604 | 00:00 |
| 11 | 0.530755 | 2.363345 | 0.570231 | 00:01 |
| 12 | 0.496605 | 2.369959 | 0.572347 | 00:01 |
| 13 | 0.475748 | 2.354409 | 0.575195 | 00:00 |
| 14 | 0.464646 | 2.367406 | 0.573486 | 00:00 |
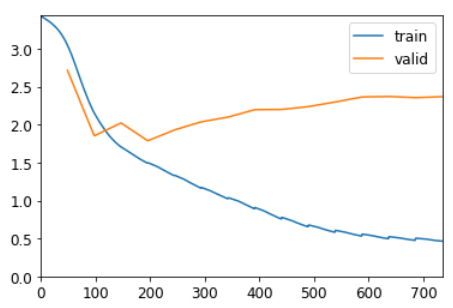
Это разочаровывает ... наша предыдущая однослойная RNN работала лучше. Почему? Причина в том, что у нас есть более глубокая модель, ведущая к взрывным или исчезающим активациям.
Взрывающиеся или исчезающие активации
На практике создание точных моделей из таких RNN затруднительно. Мы получим лучшие результаты, если будем вызывать detach реже и иметь больше уровней - это дает нашей RNN более длительный временной горизонт, на котором можно учиться, и более богатые функции для создания. Но это также означает, что нам нужно тренировать более глубокую модель. Ключевой задачей в развитии глубокого обучения было выяснить, как обучать такие модели.
Причина, по которой это сложно, в том, что происходит, когда вы умножаете на матрицу много раз. Подумайте, что произойдет, если вы умножите на число много раз. Например, если вы умножите на 2, начиная с 1, вы получите последовательность 1, 2, 4, 8, ... после 32 шагов вы уже на уровне 4 294 967 296. Аналогичная проблема возникает, если вы умножаете на 0,5: вы получаете 0,5, 0,25, 0,125… и после 32 шагов это 0,00000000023. Как видите, умножение на число, даже немного большее или меньшее, чем 1, приводит к взрыву или исчезновению нашего начального числа после нескольких повторных умножений.
Поскольку умножение матриц - это просто умножение чисел и их сложение, то же самое происходит и с повторяющимися умножениями матриц. И это все, чем является глубокая нейронная сеть - каждый дополнительный слой - это еще одно умножение матриц. Это означает, что глубокая нейронная сеть может легко получить очень большие или очень маленькие числа.
Это проблема, потому что способ, которым компьютеры хранят числа (известный как «плавающая точка»), означает, что они становятся все менее и менее точными по мере удаления чисел от нуля. Диаграмма в < > из отличной статьи «Что вы никогда не хотели знать о плавающей запятой, но вам придется узнать» ,( "What You Never Wanted to Know About Floating Point but Will Be Forced to Find Out") показывает, как точность чисел с плавающей запятой изменяется по числовой строке.
Эта неточность означает, что часто градиенты, вычисленные для обновления весов, в конечном итоге равны нулю или бесконечности для глубоких сетей. Это обычно называется проблемой исчезающих градиентов или взрывных градиентов . Это означает, что в SGD веса либо вообще не обновляются, либо перескакивают на бесконечность. В любом случае они не станут лучше тренироваться.
Исследователи разработали несколько способов решения этой проблемы, которые мы обсудим позже в книге. Один из вариантов - изменить определение слоя таким образом, чтобы снизить вероятность его взрывных активаций. Мы рассмотрим детали того, как это делается, в < >, когда мы обсуждаем пакетную нормализацию, и < >, когда мы обсуждаем ResNets, хотя эти детали обычно не имеют значения на практике (если вы не исследователь, который создает новые подходы к решению этой проблемы). Другая стратегия решения этой проблемы - осторожность при инициализации, которую мы исследуем в < >.
Для RNN есть два типа слоев, которые часто используются, чтобы избежать взрывных активаций: стробированные повторяющиеся единицы (GRU) и уровни долговременной краткосрочной памяти (LSTM). Оба они доступны в PyTorch и являются заменой для уровня RNN. В этой книге мы будем рассматривать только LSTM; в Интернете есть множество хороших руководств, объясняющих GRU, которые являются второстепенным вариантом конструкции LSTM.
LSTM
LSTM - это архитектура, которая была представлена еще в 1997 году Юргеном Шмидхубером и Зеппом Хохрайтером. В этой архитектуре есть не одно, а два скрытых состояния. В нашей базовой RNN скрытое состояние - это выход RNN на предыдущем временном шаге. Это скрытое состояние отвечает за две вещи:
- Наличие правильной информации для выходного слоя, чтобы предсказать правильный следующий токен
- Сохраняя в памяти все, что произошло в приговоре
Рассмотрим, например, предложения «У Генри есть собака, и он очень любит свою собаку» и «У Софи есть собака, и она очень любит свою собаку». Это очень ясно , что RNN нужно помнить имя в начале предложения , чтобы быть в состоянии предсказать , что он / она или его / ее .
На практике RNN действительно плохо сохраняют память о том, что произошло намного раньше в предложении, что является мотивацией иметь другое скрытое состояние (называемое состоянием ячейки ) в LSTM. Состояние ячейки будет отвечать за сохранение долговременной краткосрочной памяти , а скрытое состояние будет сосредоточено на следующем токене, который нужно предсказать. Давайте подробнее рассмотрим, как это достигается, и создадим LSTM с нуля.
Создание LSTM с нуля
Чтобы построить LSTM, мы сначала должны понять его архитектуру. < > показывает его внутреннюю структуру. 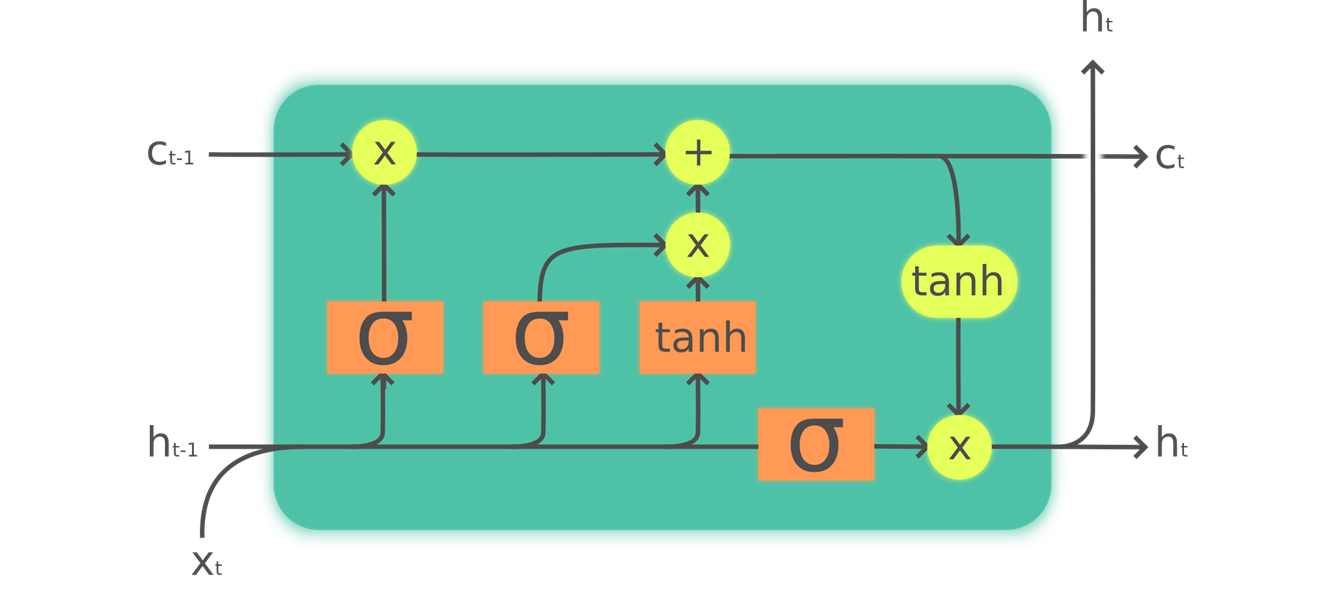
На этом рисунке наш вход входит слева с предыдущим скрытым состоянием ( $ h_ {t-1} $ ) и состоянием ячейки ( $ c_ {t-1} $ ). Четыре оранжевых прямоугольника представляют четыре слоя (наши нейронные сети) с активацией сигмовидной ( $ \ sigma $ ) или tanh. tanh - это просто сигмоидальная функция, масштабируемая до диапазона от -1 до 1. Ее математическое выражение можно записать следующим образом:
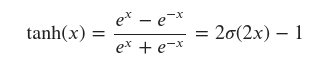
$$\tanh(x) = \frac{e^{x} - e^{-x}}{e^{x}+e^{-x}} = 2 \sigma(2x) - 1$$
где - сигмоидальная функция. Зеленые кружки - поэлементные операции. Справа отображается новое скрытое состояние ( $ h_ {t} $ ) и новое состояние ячейки ( $ c_ {t} $ ), готовые для нашего следующего ввода. Новое скрытое состояние также используется в качестве вывода, поэтому стрелка разделяется, чтобы идти вверх.σчастcт
Давайте рассмотрим четыре нейронные сети (называемые воротами ) одну за другой и объясним схему - но перед этим обратите внимание, как очень мало изменяется состояние ячейки (вверху). Он даже не проходит напрямую через нейронную сеть! Именно поэтому он будет оставаться в более долгосрочном состоянии.
Сначала стрелки для ввода и старого скрытого состояния объединяются. В RNN, которую мы писали ранее в этой главе, мы складывали их вместе. В LSTM мы складываем их в один большой тензор. Это означает, что размерность наших вложений (размерность ) может отличаться от измерения нашего скрытого состояния. Если мы назовем их n_in и n_hid, стрелка внизу будет иметь размер n_in + n_hid; таким образом, все нейронные сети (оранжевые прямоугольники) представляют собой линейные слои со n_in + n_hid входами и n_hidвыходами.
Первые ворота (если смотреть слева направо) называются воротами забвения . Поскольку это линейный слой, за которым следует сигмоид, его выходные данные будут состоять из скаляров от 0 до 1. Мы умножаем этот результат на состояние ячейки, чтобы определить, какую информацию сохранить, а какую выбросить: значения, близкие к 0, отбрасываются, а значения ближе до 1 сохранены. Это дает LSTM возможность забыть о своем долгосрочном состоянии. Например, при пересечении точки или xxbosтокена мы ожидаем, что он (научился) сбрасывать состояние своей ячейки.
Второй вентиль называется входным вентилем . Он работает с третьим вентилем (который на самом деле не имеет имени, но иногда называется вентилем ячейки ) для обновления состояния ячейки. Например, мы можем увидеть новое местоимение пола, и в этом случае нам нужно будет заменить информацию о поле, которую удалили ворота забывания. Подобно вентилю забывания, входной вентиль решает, какие элементы состояния ячейки обновлять (значения, близкие к 1) или нет (значения, близкие к 0). Третий вентиль определяет эти обновленные значения в диапазоне от –1 до 1 (благодаря функции tanh). Затем результат добавляется к состоянию ячейки.
Последний вентиль - выходной вентиль . Он определяет, какую информацию о состоянии ячейки использовать для генерации вывода. Состояние ячейки проходит через tanh перед объединением с сигмоидальным выходом из выходного вентиля, и в результате получается новое скрытое состояние.
Что касается кода, мы можем написать те же шаги, например:
class LSTMCell(Module):
def __init__(self, ni, nh):
self.forget_gate = nn.Linear(ni + nh, nh)
self.input_gate = nn.Linear(ni + nh, nh)
self.cell_gate = nn.Linear(ni + nh, nh)
self.output_gate = nn.Linear(ni + nh, nh)
def forward(self, input, state):
h,c = state
h = torch.cat([h, input], dim=1)
forget = torch.sigmoid(self.forget_gate(h))
c = c * forget
inp = torch.sigmoid(self.input_gate(h))
cell = torch.tanh(self.cell_gate(h))
c = c + inp * cell
out = torch.sigmoid(self.output_gate(h))
h = out * torch.tanh(c)
return h, (h,c)На практике мы можем затем провести рефакторинг кода. Кроме того, с точки зрения производительности лучше выполнять одно большое умножение матриц, чем четыре меньших (это потому, что мы запускаем специальное быстрое ядро на графическом процессоре только один раз, и это дает графическому процессору больше работы для параллельной работы). Наложение занимает немного времени (так как мы должны перемещать один из тензоров на графическом процессоре, чтобы получить все это в непрерывном массиве), поэтому мы используем два отдельных слоя для ввода и скрытого состояния. Оптимизированный и отремонтированный код выглядит следующим образом:
class LSTMCell(Module):
def __init__(self, ni, nh):
self.ih = nn.Linear(ni,4*nh)
self.hh = nn.Linear(nh,4*nh)
def forward(self, input, state):
h,c = state
# One big multiplication for all the gates is better than 4 smaller ones
gates = (self.ih(input) + self.hh(h)).chunk(4, 1)
ingate,forgetgate,outgate = map(torch.sigmoid, gates[:3])
cellgate = gates[3].tanh()
c = (forgetgate*c) + (ingate*cellgate)
h = outgate * c.tanh()
return h, (h,c)Здесь мы используем chunkметод PyTorch, чтобы разделить наш тензор на четыре части. Это работает так:
t = torch.arange(0,10); ttensor([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
t.chunk(2)(tensor([0, 1, 2, 3, 4]), tensor([5, 6, 7, 8, 9]))
Теперь давайте воспользуемся этой архитектурой для обучения языковой модели!
Обучение языковой модели с использованием LSTM
Вот такая же сеть, как LMModel5 и при использовании двухуровневого LSTM. Мы можем тренировать его с более высокой скоростью обучения за более короткое время и получить лучшую точность:
class LMModel6(Module):
def __init__(self, vocab_sz, n_hidden, n_layers):
self.i_h = nn.Embedding(vocab_sz, n_hidden)
self.rnn = nn.LSTM(n_hidden, n_hidden, n_layers, batch_first=True)
self.h_o = nn.Linear(n_hidden, vocab_sz)
self.h = [torch.zeros(n_layers, bs, n_hidden) for _ in range(2)]
def forward(self, x):
res,h = self.rnn(self.i_h(x), self.h)
self.h = [h_.detach() for h_ in h]
return self.h_o(res)
def reset(self):
for h in self.h: h.zero_()learn = Learner(dls, LMModel6(len(vocab), 64, 2),
loss_func=CrossEntropyLossFlat(),
metrics=accuracy, cbs=[ModelResetter,ShowGraphCallback()])
learn.fit_one_cycle(15, 1e-2)| epoch | train_loss | valid_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 3.013884 | 2.711881 | 0.413656 | 00:01 |
| 1 | 2.225005 | 2.139775 | 0.180501 | 00:01 |
| 2 | 1.650055 | 2.218482 | 0.373291 | 00:01 |
| 3 | 1.347298 | 1.839942 | 0.449463 | 00:01 |
| 4 | 1.086787 | 1.977849 | 0.475993 | 00:01 |
| 5 | 0.850407 | 1.867124 | 0.559489 | 00:01 |
| 6 | 0.614563 | 1.435763 | 0.581624 | 00:01 |
| 7 | 0.423366 | 1.109806 | 0.657796 | 00:01 |
| 8 | 0.292623 | 1.315230 | 0.679769 | 00:01 |
| 9 | 0.227730 | 1.205368 | 0.702230 | 00:01 |
| 10 | 0.184233 | 1.176871 | 0.739502 | 00:01 |
| 11 | 0.147610 | 1.199790 | 0.731689 | 00:01 |
| 12 | 0.120146 | 1.186787 | 0.742188 | 00:01 |
| 13 | 0.103536 | 1.174540 | 0.736165 | 00:01 |
| 14 | 0.095180 | 1.169136 | 0.741211 | 00:01 |
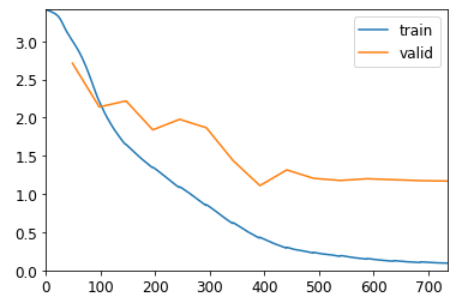
Это лучше, чем многослойная RNN! Однако мы все еще можем видеть, что есть небольшая переобучение, что является признаком того, что небольшая регуляризация может помочь.
Регуляризация LSTM
Рекуррентные нейронные сети, как правило, трудно обучить из-за проблемы исчезающих активаций и градиентов, которую мы видели ранее. Использование ячеек LSTM (или GRU) делает обучение проще, чем с обычными RNN, но они по-прежнему очень подвержены переобучению. Увеличение данных, хотя и возможно, реже используется для текстовых данных, чем для изображений, потому что в большинстве случаев для генерации случайных дополнений требуется другая модель (например, путем перевода текста на другой язык, а затем обратно на исходный язык). В целом, расширение данных для текстовых данных в настоящее время не является хорошо изученной областью.
Однако есть другие методы регуляризации, которые мы можем использовать вместо этого для уменьшения переобучения, которые были тщательно изучены для использования с LSTM в статье Стивена Мерити, Нитиша Шириша Кескара и Ричарда Сошера «Регуляризация и оптимизация языковых моделей LSTM» .("Regularizing and Optimizing LSTM Language Models") В данной статье показано , как эффективное использование отсева , активация регуляризации и временной регуляризация активации может позволить LSTM к биениям внедренных результатов , которые раньше требовали гораздо более сложных моделей. Авторы назвали LSTM, использующий эти методы, AWD-LSTM . Мы рассмотрим каждый из этих методов по очереди.
Dropout
Dropout - это метод регуляризации, который был предложен Джеффри Хинтоном и др. в Улучшение нейронных сетей за счет предотвращения совместной адаптации детекторов признаков . Основная идея состоит в том, чтобы случайным образом обнулить некоторые активации во время обучения. Это гарантирует, что все нейроны активно работают в направлении вывода, как показано в < > (из «Отсев: простой способ предотвратить переоснащение нейронных сетей» Нитиша Шриваставы и др.).
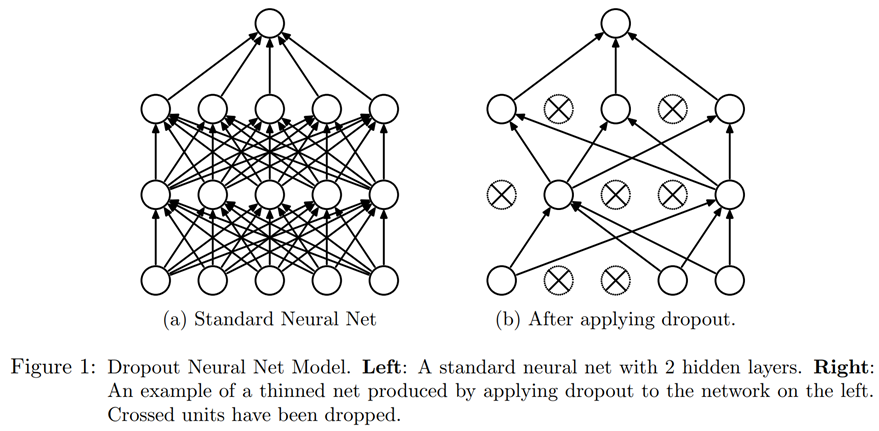
Хинтон использовал красивую метафору, когда в интервью объяснил причины, по которым бросил учебу:
: Я пошел в свой банк. Служащие менялись, и я спросил одного из них, почему. Он сказал, что не знает, но их часто меняют. Я подумал, что это должно быть потому, что для успешного обмана банка потребуется сотрудничество между сотрудниками. Это заставило меня понять, что случайное удаление разных подмножеств нейронов в каждом примере предотвратит заговоры и, таким образом, уменьшит переобучение.
В том же интервью он также объяснил, что нейробиология дала дополнительное вдохновение:
: Мы действительно не знаем, почему нейроны разрастаются. Одна из теорий состоит в том, что они хотят зашумить, чтобы упорядочить, потому что у нас гораздо больше параметров, чем точек данных. Идея отсева заключается в том, что если у вас есть шумные активации, вы можете позволить себе использовать гораздо большую модель.
Это объясняет идею, по которой отсев помогает обобщать: сначала он помогает нейронам лучше взаимодействовать друг с другом, затем он делает активацию более шумной, что делает модель более устойчивой.
Однако мы можем видеть, что, если бы мы просто обнулили эти активации, не делая ничего другого, у нашей модели были бы проблемы с обучением: если мы перейдем от суммы пяти активаций (все они являются положительными числами, поскольку мы применяем ReLU), чтобы просто во-вторых, у этого не будет того же масштаба. Поэтому, если мы применяем отсев с вероятностью p, мы изменяем масштаб всех активаций, разделив их на 1-p(в среднем pбудет обнулено, поэтому он уйдет 1-p), как показано в < >.
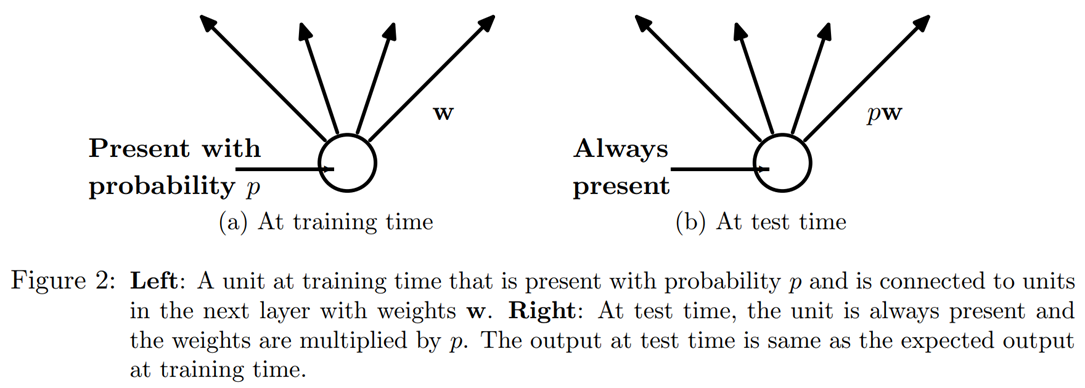
Это полная реализация слоя исключения(Dropout) в PyTorch (хотя собственный уровень PyTorch фактически написан на C, а не на Python):
class Dropout(Module):
def __init__(self, p): self.p = p
def forward(self, x):
if not self.training: return x
mask = x.new(*x.shape).bernoulli_(1-p)
return x * mask.div_(1-p)bernoulli_ Метод создает тензор случайных нулей (с вероятностью p) и единиц (с вероятностью 1-p), который затем умножают на нашем ввода перед делением 1-p. Обратите внимание на использование trainingатрибута, который доступен в любом PyTorch nn.Module, и сообщает нам, проводим ли мы обучение или вывод.
примечание: проводите собственные эксперименты: в предыдущих главах книги мы добавляли здесь пример кода bernoulli_, чтобы вы могли точно увидеть, как это работает. Но теперь, когда вы знаете достаточно, чтобы делать это самостоятельно, мы будем делать для вас все меньше и меньше примеров и вместо этого будем ожидать, что вы проведете свои собственные эксперименты, чтобы увидеть, как все работает. В этом случае вы увидите вопросник в конце главы, с которым мы просим вас поэкспериментировать, bernoulli_ но не ждите, пока мы попросим вас поэкспериментировать, чтобы развить ваше понимание кода, который мы изучаем; давай и сделай это в любом случае!
Использование dropout перед передачей вывода нашего LSTM на последний уровень поможет уменьшить переобучение. Dropout также используется во многих других моделях, включая используемую по умолчанию заголовок CNN fastai.vision, и доступен fastai.tabular при передаче psпараметра (где каждый «p» передается каждому добавленному Dropoutуровню), как мы увидим в < >.
Dropout ведет себя по-разному в режиме обучения и проверки, который мы указали с помощью training атрибута в Dropout. Вызов train метода в a Module устанавливает training значение True(как для модуля, в котором вы вызываете метод, так и для каждого модуля, который он рекурсивно содержит), и evalустанавливает его в False. Это делается автоматически при вызове методов Learner, но если вы не используете этот класс, не забудьте переключаться с одного на другой по мере необходимости.
Регуляризация активации и регуляризация временной активации
Регуляризация активации (AR) и регуляризация временной активации (TAR) - это два метода регуляризации, очень похожие на снижение веса, обсуждаемые в < >. Применяя снижение веса, мы добавляем небольшой штраф к потере, чтобы сделать веса как можно меньше. Для регуляризации активации мы постараемся сделать как можно меньшие конечные активации, производимые LSTM, а не веса.
Чтобы упорядочить окончательные активации, мы должны где-то их сохранить, а затем прибавить средние их квадратов к потерям (вместе с множителем alpha, что аналогично wdснижению веса):
loss += alpha * activations.pow(2).mean()Регуляризация временной активации связана с тем, что мы прогнозируем токены в предложении. Это означает, что, вероятно, выходные данные наших LSTM должны иметь некоторый смысл, когда мы читаем их по порядку. TARпризван стимулировать такое поведение, добавляя штраф к потерям, чтобы разница между двумя последовательными активациями была как можно меньше: наш тензор активаций имеет форму bs x sl x n_hid, и мы считываем последовательные активации на оси длины последовательности (размер посередине ). При этом TAR можно выразить как:
loss += beta * (activations[:,1:] - activations[:,:-1]).pow(2).mean()alpha и beta затем нужно настроить два гиперпараметра. Чтобы это работало, нам нужна наша модель с выпадением, чтобы возвращать три вещи: правильный вывод, активацию предварительного выпадения LSTM и активацию пост-выпадения LSTM. AR часто применяется к выпавшим активациям (чтобы не наказывать активации, которые мы впоследствии превратили в нули), в то время как TAR применяется к не выпавшим активациям (потому что эти нули создают большие различия между двумя последовательными временными шагами). Затем вызывается обратный вызов RNNRegularizer, который применяет для нас эту регуляризацию.
Тренировка регулируемого LSTM с отягощениями
Мы можем комбинировать выпадение (применяемое до перехода на наш выходной слой) с AR и TAR для обучения нашей предыдущей LSTM. Нам просто нужно вернуть три вещи вместо одной: нормальный вывод нашего LSTM, выпавшие активации и активации из наших LSTM. Последние два будут забраны обратным вызовом RNNRegularization за вклады, которые он должен внести в убыток.
Еще один полезный трюк, который мы можем добавить из AWD LSTM, - это связывание по весу . В языковой модели входные вложения представляют собой сопоставление английских слов с активациями, а выходной скрытый слой представляет собой сопоставление активаций с английскими словами. Интуитивно мы могли бы ожидать, что эти сопоставления могут быть такими же. Мы можем представить это в PyTorch, назначив одну и ту же весовую матрицу каждому из этих слоев:
self.h_o.weight = self.i_h.weight
В LMModel7, мы включаем эти последние настройки:
class LMModel7(Module):
def __init__(self, vocab_sz, n_hidden, n_layers, p):
self.i_h = nn.Embedding(vocab_sz, n_hidden)
self.rnn = nn.LSTM(n_hidden, n_hidden, n_layers, batch_first=True)
self.drop = nn.Dropout(p)
self.h_o = nn.Linear(n_hidden, vocab_sz)
self.h_o.weight = self.i_h.weight
self.h = [torch.zeros(n_layers, bs, n_hidden) for _ in range(2)]
def forward(self, x):
raw,h = self.rnn(self.i_h(x), self.h)
out = self.drop(raw)
self.h = [h_.detach() for h_ in h]
return self.h_o(out),raw,out
def reset(self):
for h in self.h: h.zero_()Мы можем создать регуляризацию Learnerс помощью RNNRegularizer обратного вызова:
learn = Learner(dls, LMModel7(len(vocab), 64, 2, 0.4),
loss_func=CrossEntropyLossFlat(), metrics=accuracy,
cbs=[ModelResetter, RNNRegularizer(alpha=2, beta=1)])A TextLearner автоматически добавляет для нас эти два обратных вызова (с этими значениями для alpha и beta по умолчанию), поэтому мы можем упростить предыдущую строку до:
learn = TextLearner(dls, LMModel7(len(vocab), 64, 2, 0.4),
loss_func=CrossEntropyLossFlat(), metrics=accuracy,cbs=ShowGraphCallback())Затем мы можем обучить модель и добавить дополнительную регуляризацию, увеличив спад веса до 0.1:
learn.fit_one_cycle(15, 1e-2, wd=0.1)| epoch | train_loss | valid_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 2.544806 | 1.913321 | 0.484945 | 00:01 |
| 1 | 1.568985 | 1.177975 | 0.643799 | 00:01 |
| 2 | 0.831121 | 0.763713 | 0.768717 | 00:01 |
| 3 | 0.414470 | 0.738221 | 0.797445 | 00:01 |
| 4 | 0.213541 | 0.503155 | 0.860677 | 00:01 |
| 5 | 0.123785 | 0.455092 | 0.859131 | 00:01 |
| 6 | 0.074512 | 0.413049 | 0.872314 | 00:01 |
| 7 | 0.048507 | 0.461668 | 0.868815 | 00:01 |
| 8 | 0.035071 | 0.434570 | 0.866781 | 00:01 |
| 9 | 0.027789 | 0.376141 | 0.889079 | 00:01 |
| 10 | 0.022220 | 0.354690 | 0.896891 | 00:01 |
| 11 | 0.017890 | 0.369849 | 0.892578 | 00:01 |
| 12 | 0.015125 | 0.372715 | 0.891439 | 00:01 |
| 13 | 0.013198 | 0.363804 | 0.894124 | 00:01 |
| 14 | 0.011936 | 0.358279 | 0.896403 | 00:01 |
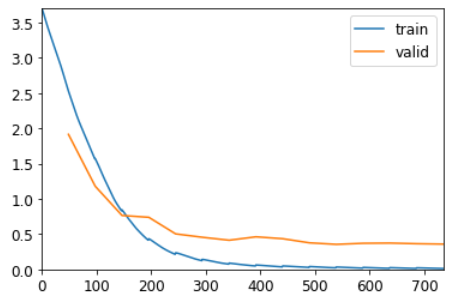
learn.fit_one_cycle(5, 2e-3, wd=0.5)| epoch | train_loss | valid_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 0.008226 | 0.662939 | 0.872396 | 00:01 |
| 1 | 0.012891 | 0.652557 | 0.874837 | 00:01 |
| 2 | 0.012473 | 0.573693 | 0.879232 | 00:01 |
| 3 | 0.011584 | 0.500434 | 0.890137 | 00:01 |
| 4 | 0.010289 | 0.523193 | 0.882650 | 00:01 |
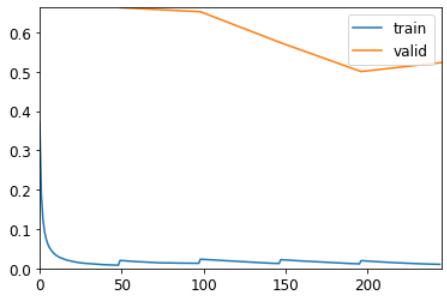
# learn.summary()Теперь это намного лучше, чем наша предыдущая модель!
Вывод
Теперь вы увидели все, что находится внутри архитектуры AWD-LSTM, которую мы использовали при классификации текста в < >. Он использует отсев в гораздо большем количестве мест:
- Отключение встраивания (сразу после слоя встраивания)
- Отключение ввода (после слоя внедрения)
- Падение веса (применяется к весам LSTM на каждом этапе тренировки)
- Скрытый выпадение (применяется к скрытому состоянию между двумя слоями)
Это делает его еще более упорядоченным. Поскольку точная настройка этих пяти значений отсева (включая отсев перед выходным слоем) сложна, мы определили хорошие значения по умолчанию и позволили настроить величину отсева в целом с помощью drop_mult параметра, который вы видели в этой главе (который умножается на каждое выпадение). ).
Еще одна очень мощная архитектура, особенно в задачах «от последовательности к последовательности» (то есть задач, в которых зависимая переменная сама по себе является последовательностью переменной длины, такой как языковой перевод), - это архитектура Transformers. Вы можете найти его в бонусной главе на сайте книги .
Опросник
- Что делать, если набор данных для вашего проекта настолько велик и сложен, что работа с ним требует значительного количества времени?
- Почему мы объединяем документы в нашем наборе данных перед созданием языковой модели?
- Какие две настройки нам нужно внести в нашу модель, чтобы использовать стандартную полностью подключенную сеть для предсказания четвертого слова с учетом предыдущих трех слов?
- Как мы можем использовать весовую матрицу для нескольких слоев в PyTorch?
- Напишите модуль, который предсказывает третье слово по двум предыдущим словам предложения, не подглядывая.
- Что такое рекуррентная нейронная сеть?
- Что такое «скрытое состояние»?
- В чем эквивалент скрытого состояния LMModel1?
- Почему для поддержания состояния в RNN важно передавать текст в модель по порядку?
- Что такое «развернутое» представление RNN?
- Почему поддержание скрытого состояния в RNN может привести к проблемам с памятью и производительностью? Как решить эту проблему?
- Что такое «BPTT»?
- Напишите код для печати первых нескольких пакетов проверочного набора, включая преобразование идентификаторов токенов обратно в английские строки, как мы показали для пакетов данных IMDb в < >.
- Что делает ModelResetterобратный вызов? Зачем нам это нужно?
- Каковы недостатки предсказания только одного выходного слова на каждые три входных слова?
- Зачем нужна настраиваемая функция потерь для LMModel4?
- Почему обучение LMModel4нестабильно?
- В развернутом представлении мы видим, что рекуррентная нейронная сеть на самом деле имеет много слоев. Итак, почему нам нужно объединять RNN, чтобы получить лучшие результаты?
- Изобразите составную (многослойную) RNN.
- Почему мы должны добиваться лучших результатов в RNN, если мы звоним detachреже? Почему на практике этого не происходит с простой RNN?
- Почему глубокая сеть может приводить к очень большим или очень маленьким активациям? Почему это важно?
- Какие числа наиболее точны в компьютерном представлении чисел с плавающей запятой?
- Почему исчезающие градиенты мешают обучению?
- Почему помогает наличие двух скрытых состояний в архитектуре LSTM? Какова цель каждого из них?
- Как эти два состояния называются в LSTM?
- Что такое tanh и как оно связано с сигмовидной кишкой?
- Какова цель этого кода LSTMCell:h = torch.cat([h, input], dim=1)
- Что делает chunkв PyTorch?
- LSTMCellВнимательно изучите реорганизованную версию, чтобы убедиться, что вы понимаете, как и почему она делает то же самое, что и версия без рефакторинга.
- Почему мы можем использовать более высокую скорость обучения LMModel6?
- Какие три метода регуляризации используются в модели AWD-LSTM?
- Что такое «отсев»?
- Почему мы масштабируем веса при отсеве? Применяется ли это во время обучения, вывода или и того, и другого?
- Какова цель этой строки Dropout:if not self.training: return x
- Поэкспериментируйте, bernoulli_чтобы понять, как это работает.
- Как перевести модель в режим обучения в PyTorch? В режиме оценки?
- Напишите уравнение регуляризации активации (математикой или кодом, как вам удобнее). Чем это отличается от снижения веса?
- Напишите уравнение для регуляризации временной активации (математикой или кодом, как вам удобнее). Почему бы нам не использовать это для проблем с компьютерным зрением?
- Что такое «привязка веса» к языковой модели?
Дальнейшие исследования
- Во LMModel2, с чего forwardначать h=0? Почему нам не нужно говорить h=torch.zeros(...)?
- Напишите код для LSTM с нуля (вы можете обратиться к < >).
- Поищите в Интернете архитектуру GRU и реализуйте ее с нуля, а затем попробуйте обучить модель. Посмотрите, сможете ли вы получить результаты, аналогичные тем, которые мы видели в этой главе. Сравните свои результаты с результатами встроенного GRU модуля PyTorch .
- Взгляните на исходный код AWD-LSTM в fastai и попробуйте сопоставить каждую из строк кода с концепциями, показанными в этой главе.
Метки
Раскрыть комментарии 0
Чтобы оставить комментарий , Вам необходимо Авторизоваться или пройти Регистрацию



