import fastbook
fastbook.setup_book()#hide
from fastai.vision.all import *
from fastbook import *
matplotlib.rc('image', cmap='Greys')Под капотом: обучение классификатора цифр
Увидев, как на самом деле выглядит обучение различных моделей в главе 2, давайте теперь заглянем под капот и точно посмотрим, что происходит. Мы начнем с использования компьютерного зрения, чтобы познакомить с фундаментальными инструментами и концепциями глубокого обучения.
Если быть точным, мы обсудим роли массивов и тензоров, а также широковещательную передачу, мощный метод их выразительного использования. Мы объясним стохастический градиентный спуск (SGD), механизм обучения путем автоматического обновления весов. Мы обсудим выбор функции потерь для нашей основной задачи классификации и роль мини-пакетов. Мы также опишем математику, которую фактически выполняет базовая нейронная сеть. Наконец, мы соберем все эти части вместе.
В будущих главах мы также будем глубоко погружаться в другие приложения и посмотрим, как эти концепции и инструменты обобщаются. Но в этой главе речь идет о закладке камней основания. Откровенно говоря, это также делает эту главу одной из самых сложных, поскольку все эти понятия зависят друг от друга. Как арка, все камни должны быть на месте, чтобы структура оставалась на высоте. "Это требует некоторого терпения, чтобы собраться.
Начнем. Первым шагом является рассмотрение того, как изображения представлены в компьютере.
Пиксели: основы компьютерного зрения
Чтобы понять, что происходит в модели компьютерного зрения, мы сначала должны понять, как компьютеры обрабатывают изображения. Для наших экспериментов мы будем использовать один из самых известных наборов данных в области компьютерного зрения, MNIST . MNIST содержит изображения рукописных цифр, собранные Национальным институтом стандартов и технологий и объединенные в набор данных машинного обучения Янном Лекуном и его коллегами. Лекун использовал MNIST в 1998 году в Lenet-5 , первой компьютерной системе, демонстрирующей практически полезное распознавание рукописных последовательностей цифр. Это было одно из самых важных достижений в истории искусственного интеллекта.
Боковая панель (Sidebar): упорство и глубокое обучение
История глубокого обучения - это история упорства и стойкости горстки преданных своему делу исследователей. После первых надежд (и шумихи!) Нейронные сети вышли из моды в 1990-х и 2000-х годах, и лишь горстка исследователей пыталась заставить их работать хорошо. Трое из них, Ян Лекун, Йошуа Бенджио и Джеффри Хинтон, были удостоены высшей награды в области информатики - премии Тьюринга (обычно считающейся «Нобелевской премией по информатике») в 2018 году после победы, несмотря на глубокий скептицизм сообщества машинного обучения и статистики.
Джефф Хинтон рассказал, что даже научные статьи, показывающие значительно лучшие результаты, чем все ранее опубликованные, будут отклонены ведущими журналами и конференциями только потому, что они использовали нейронную сеть. Работа Яна Лекуна над сверточными нейронными сетями, которую мы изучим в следующем разделе, показала, что эти модели могут читать рукописный текст - чего никогда раньше не было. Однако его открытие было проигнорировано большинством исследователей, даже несмотря на то, что его использовали в коммерческих целях для чтения 10% чеков в США!
Помимо этих трех обладателей премии Тьюринга, есть много других исследователей, которые боролись за то, чтобы привести нас туда, где мы находимся сегодня. Например, Юрген Шмидхубер (который, по мнению многих, должен был стать участником Премии Тьюринга) был пионером многих важных идей, включая работу со своим учеником Зеппом Хохрайтером над архитектурой долговременной краткосрочной памяти (LSTM) (широко используемой для распознавания речи и другого моделирования текста. Используется в примере IMDb в < >). Возможно, наиболее важным из всех, Пол Вербос в 1974 году изобрел обратное распространение для нейронных сетей, техника, показанная в этой главе и используемая повсеместно для обучения нейронных сетей ( Werbos 1994 ). Его развитие почти полностью игнорировалось десятилетиями, но сегодня оно считается важнейшим фундаментом современного ИИ.
Это урок для всех нас! На пути к глубокому обучению вы столкнетесь со многими препятствиями, как техническими, так и (что еще более сложными), создаваемыми окружающими вас людьми, которые не верят, что вы добьетесь успеха. Есть один гарантированный способ провалиться - это прекратить попытки. Мы видели, что единственная последовательная черта среди каждого fast.ai студента, который стал практиком мирового уровня, это то, что все они очень настойчивы.
Конечная боковая панель (End sidebar)
Для этого начального учебного пособия мы просто попытаемся создать модель, которая может классифицировать любое изображение как 3 или 7. Давайте загрузим образец MNIST, который содержит изображения только этих цифр:
path = untar_data(URLs.MNIST_SAMPLE)#hide
Path.BASE_PATH = pathМы можем увидеть, что находится в этом каталоге, используя ls, метод, добавленный fastai. Этот метод возвращает объект специального класса fastai под названием L, который имеет все те же функциональные возможности встроенного списка Python, плюс гораздо больше. Одной из его удобных особенностей является то, что при печати он отображает количество предметов, перед перечислением самих предметов (если их более 10 предметы, он просто показывает первые несколько):
path.ls()(#3) [Path('train'),Path('valid'),Path('labels.csv')]
Набор данных MNIST следует общей схеме для наборов данных машинного обучения: отдельные папки для обучающего набора и набора проверки (и / или набора тестов). Посмотрим, что внутри обучающего набора:
(path/'train').ls()(#2) [Path('train/7'),Path('train/3')]
Существует папка 3 и папка 7. На языке машинного обучения мы говорим, что «3» и «7» являются метками (или целями) в этом наборе данных. Давайте рассмотрим одну из этих папок (используя сортировку, чтобы гарантировать, что мы все получаем один и тот же порядок файлов):
threes = (path/'train'/'3').ls().sorted()
sevens = (path/'train'/'7').ls().sorted()
threes(#6131) [Path('train/3/10.png'),Path('train/3/10000.png'),Path('train/3/10011.png'),Path('train/3/10031.png'),Path('train/3/10034.png'),Path('train/3/10042.png'),Path('train/3/10052.png'),Path('train/3/1007.png'),Path('train/3/10074.png'),Path('train/3/10091.png')...]
Как и следовало ожидать, он полон файлов изображений. Давайте посмотрим на один сейчас. Вот изображение написанной от руки цифры 3, взятой из известного набора данных MNIST с рукописными числами:
im3_path = threes[1]
im3 = Image.open(im3_path)
im3
Здесь мы используем Imageкласс из Python Imaging Library (PIL), который является наиболее широко используемым пакетом Python для открытия, управления и просмотра изображений. Jupyter знает об изображениях PIL, поэтому он автоматически отображает их.
В компьютере все представлено в виде чисел. Чтобы просмотреть числа, составляющие это изображение, мы должны преобразовать его в массив NumPy или тензор PyTorch . Например, вот как выглядит часть изображения, преобразованная в массив NumPy:
array(im3)[4:10,4:10]array([[ 0, 0, 0, 0, 0, 0],
[ 0, 0, 0, 0, 0, 29],
[ 0, 0, 0, 48, 166, 224],
[ 0, 93, 244, 249, 253, 187],
[ 0, 107, 253, 253, 230, 48],
[ 0, 3, 20, 20, 15, 0]], dtype=uint8)
Значение 4:10 указывает, что мы запросили строки от индекса 4 (включено) до 10 (не включено) и то же самое для столбцов. NumPy индексирует сверху вниз и слева направо, поэтому этот раздел расположен в левом верхнем углу изображения. Вот то же самое, что тензор PyTorch:
tensor(im3)[4:10,4:10]tensor([[ 0, 0, 0, 0, 0, 0],
[ 0, 0, 0, 0, 0, 29],
[ 0, 0, 0, 48, 166, 224],
[ 0, 93, 244, 249, 253, 187],
[ 0, 107, 253, 253, 230, 48],
[ 0, 3, 20, 20, 15, 0]], dtype=torch.uint8)
Мы можем разрезать массив, чтобы выбрать только ту часть, в которой находится верхняя часть цифры, а затем использовать Pandas DataFrame, чтобы закодировать значения с помощью градиента, который ясно показывает, как изображение создается из значений пикселей:
#hide_output
im3_t = tensor(im3)
df = pd.DataFrame(im3_t[4:15,4:22])
df.style.set_properties(**{'font-size':'6pt'}).background_gradient('Greys')| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 29 | 150 | 195 | 254 | 255 | 254 | 176 | 193 | 150 | 96 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 48 | 166 | 224 | 253 | 253 | 234 | 196 | 253 | 253 | 253 | 253 | 233 | 0 | 0 | 0 |
| 3 | 0 | 93 | 244 | 249 | 253 | 187 | 46 | 10 | 8 | 4 | 10 | 194 | 253 | 253 | 233 | 0 | 0 | 0 |
| 4 | 0 | 107 | 253 | 253 | 230 | 48 | 0 | 0 | 0 | 0 | 0 | 192 | 253 | 253 | 156 | 0 | 0 | 0 |
| 5 | 0 | 3 | 20 | 20 | 15 | 0 | 0 | 0 | 0 | 0 | 43 | 224 | 253 | 245 | 74 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 249 | 253 | 245 | 126 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 14 | 101 | 223 | 253 | 248 | 124 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 | 11 | 166 | 239 | 253 | 253 | 253 | 187 | 30 | 0 | 0 | 0 | 0 | 0 |
| 9 | 0 | 0 | 0 | 0 | 0 | 16 | 248 | 250 | 253 | 253 | 253 | 253 | 232 | 213 | 111 | 2 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 43 | 98 | 98 | 208 | 253 | 253 | 253 | 253 | 187 | 22 | 0 |
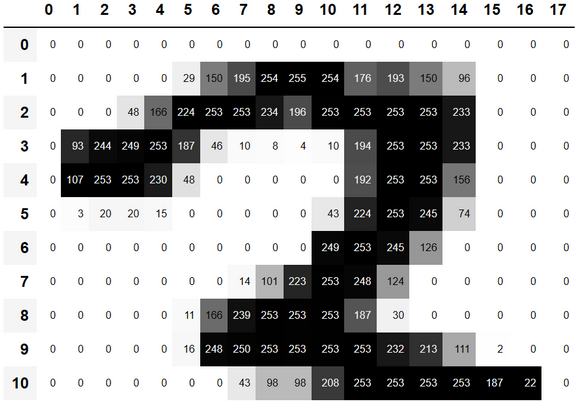
Видно, что фоновые белые пикселы хранятся как число 0, черные - как число 255, а оттенки серого - между ними. Все изображение содержит 28 пикселей в поперечном направлении и 28 пикселей вниз, в общей сложности 784 пикселя. (Это намного меньше, чем изображение, которое вы получили бы с камеры телефона, которая имеет миллионы пикселей, но является удобным размером для нашего начального обучения и экспериментов. Скоро мы создадим более крупные полноцветные изображения.)
Итак, теперь вы увидели, как изображение выглядит на компьютере, давайте вспомним нашу цель: создать модель, которая может распознавать тройки и семерки. Как бы вы могли заставить компьютер делать это?
Предупреждение: остановитесь и подумайте! Перед тем как продолжить чтение, подумайте, как компьютер может распознать эти две разные цифры. На какие особенности он может смотреть? Как он мог бы идентифицировать эти особенности? Как он мог объединить их вместе? Обучение работает лучше всего, когда вы пытаетесь решать проблемы самостоятельно, а не просто читаете чьи-то ответы; так что отойдите от этой книги на несколько минут, возьмите лист бумаги и ручку и запишите несколько идей ...
Первая попытка: сходство пикселей
Итак, вот первая идея: как найти среднее значение пикселя для каждого пикселя 3-ки, а затем сделать то же самое для 7-ки. Это даст нам два средних групповых значения, определяющих то, что мы могли бы назвать «идеальными» 3 и 7. Затем, чтобы классифицировать изображение как одну цифру или другую, мы видим, на какую из этих двух идеальных цифр изображение больше всего похоже. Это, безусловно лучше, чем ничего, поэтому начнем с этого.
жаргон: Базовый уровень: это простейшая модель, которая должна работать достаточно хорошо. Это должно быть очень просто в реализации, и очень легко в проверке, так что вы можете затем проверить каждую из ваших улучшенных идей, и убедиться, что они всегда лучше, чем ваш базовый. Не начав с разумного базового уровня, очень трудно узнать, действительно ли ваши супер-модные модели хороши. Один из хороших подходов к созданию базового уровня заключается в том, чтобы сделать то, что мы сделали здесь: придумать простую в реализации модель. Другим хорошим подходом является поиск других людей, которые решили подобные с вашими проблемы.Загрузка и запуск их кода на вашем наборе данных. В идеале, попробуйте оба!
Первым шагом для нашей простой модели является получение среднего значения пикселя для каждой из цифр. В процессе этого мы узнаем много интересных трюков программирования Python!
Давайте создадим тензор, содержащий все наши 3-ки, сложенные вместе. Мы уже знаем, как создать тензор, содержащий одно изображение. Чтобы создать тензор, содержащий все изображения в каталоге, мы сначала используем понимание списка Python для создания простого списка тензоров одного изображения.
Мы будем использовать Jupyter, чтобы сделать некоторые небольшие проверки нашей работы - в данном случае, убедившись, что количество возвращенных элементов приемлено:
seven_tensors = [tensor(Image.open(o)) for o in sevens]
three_tensors = [tensor(Image.open(o)) for o in threes]
len(three_tensors),len(seven_tensors)(6131, 6265)
Примечание. Составление списков: понимание списков и словарей - замечательная особенность Python. Многие программисты Python используют их каждый день, включая авторов этой книги - они являются частью «идиоматического Python». Но программисты, пришедшие из других языков, возможно, никогда их раньше не видели. Есть много отличных руководств, которые можно найти в Интернете, поэтому мы не будем тратить много времени на их обсуждение. Вот краткое объяснение и пример. Понимание списка выглядит следующим образом : new_list = [f(o) for o in a_list if o>0].Это вернет каждый элемент a_list, который больше 0, после передачи его функции f. Здесь есть три части: коллекция, над которой вы итерируете (a_list), необязательный фильтр (if o>0), и то, что нужно сделать с каждым элементом (f (o)). Это не только короче, но и быстрее, чем альтернативные способы создания одного и того же списка с циклом.
Мы также проверим, что одно из изображений выглядит хорошо. Поскольку теперь у нас есть тензоры (которые Jupyter по умолчанию будет печатать как значения), а не изображения PIL (которые Jupyter по умолчанию будет отображать как изображения), нам нужно использовать функцию show_image fastai для отображения:
show_image(three_tensors[1]);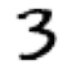
Для каждой позиции пикселя мы хотим вычислить среднее значение по всем изображениям интенсивности этого пикселя. Для этого сначала объединяем все изображения в этом списке в единый трехмерный тензор. Самый распространенный способ описать такой тензор - назвать его тензором ранга-3. Нам часто нужно складывать отдельные тензоры коллекции в один тензор. Неудивительно, что PyTorch поставляется с функцией, называемой стеком stack, которую мы можем использовать для этой цели.
Некоторые операции в PyTorch, такие как взятие среднего mean, требуют, чтобы мы превратили наши целочисленные (int) типы в плавающие(float) типы. Так как нам это понадобится позже, мы также приведем наш сложенный тензор, к типу float . Приведение в PyTorch так же просто, как ввод имени типа, к которому вы хотите привести, и обработка его как метода.
Когда есть изображение типа float, ожидается, что значения пикселей находятся в диапазоне от 0 до 1, поэтому здесь мы разделим значения тензоров на 255:
stacked_sevens = torch.stack(seven_tensors).float()/255
stacked_threes = torch.stack(three_tensors).float()/255
stacked_threes.shapetorch.Size([6131, 28, 28])
Возможно, самым важным атрибутом тензора является его форма. Здесь указывается длина каждой оси. В нашем случае у нас есть 6131 изображений, каждое размером 28 × 28 пикселей. В этом тензоре нет ничего особенного, что говорит о том, что первая ось - это количество изображений, вторая - высота, а третья - ширина - семантика тензора полностью зависит от нас и того, как мы его конструируем. Что касается PyTorch, это просто куча цифр в памяти.
Длина формы тензора - его ранг:
len(stacked_threes.shape)3
Для вас действительно важно запомнить и практиковать эти биты тензорного жаргона: ранг - это количество осей или измерений в тензоре; форма - размер каждой оси тензора.
О: Берегись, потому что термин «измерение» иногда используется двояко. Считайте, что мы живем в «трехмерном пространстве», где физическое положение может быть описано трехмерным вектором v.ndim. Но согласно PyTorch, атрибут v.ndim(который наверняка выглядит как «число измерений» v) равен единице, а не трём! Почему? Потому что v является вектором, который является тензором первого ранга, что означает, что он имеет только одну ось (даже если эта ось имеет длину три). Другими словами, иногда размерность используется для размера оси («пространство трехмерно»); в других случаях он используется для ранга, или числа осей («матрица имеет два измерения»). Я считаю полезным перевести все утверждения в термины ранга, оси и длины, которые являются однозначными терминами.
Мы также можем получить ранг тензора напрямую с помощью ndim:
stacked_threes.ndim3
Наконец, мы можем вычислить, как выглядит идеальная тройка. Мы вычисляем средние из всех тензоров изображения путем взятия среднего вдоль 0 оси из наших сложенных тензоров. Это - размер, который индексирует по всем изображениям.
Другими словами, для каждой позиции пикселя будет вычислено среднее значение этого пикселя по всем изображениям. Результатом будет одно значение для каждой позиции пикселя или одно изображение. Вот:
mean3 = stacked_threes.mean(0)
show_image(mean3);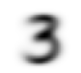
Согласно этому набору данных, это идеальное число 3 ! (Возможно, вам это не понравится, но так выглядит обобщенное представление цифры 3.). Можно увидеть что там где большинство цифр сходяться - там цвет темнее, где есть различия - там изображение тонкое и расплывчатое.
Давайте сделаем то же самое для семерки, но объединим все шаги сразу, чтобы сэкономить время:
mean7 = stacked_sevens.mean(0)
show_image(mean7);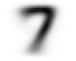
Давайте теперь возьмем произвольную тройку и измерим ее расстояние от наших «идеальных цифр».
Стоп: Остановись и подумай !: Как бы вы посчитали, насколько конкретное изображение похоже на каждую из наших идеальных цифр? Не забудьте отойти от этой книги и записать несколько идей, прежде чем двигаться дальше! Исследования показывают, что запоминание и понимание значительно улучшаются, когда вы участвуете в процессе обучения, решая проблемы, экспериментируя и пробуя новые идеи самостоятельно.
Вот образец 3:
a_3 = stacked_threes[1]
show_image(a_3);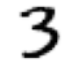
Как мы можем определить его расстояние от нашего идеального 3? Мы не можем просто сложить разницу между пикселями этого изображения и идеальной цифрой. Некоторые различия будут положительными, а другие - отрицательными, и эти различия исчезнут, что приведет к ситуации, когда изображение, которое в некоторых местах слишком темное, а в других - слишком светлое, может отображаться как имеющее нулевые общие отличия от идеального. Это было бы заблуждением!
Чтобы избежать этого, есть два основных способа измерения расстояния в этом контексте:
- Возьмите среднее значение абсолютного значения разностей (абсолютное значение - это функция, которая заменяет отрицательные значения положительными значениями). Это называется средней абсолютной разницей или нормой L1.
- Возьмите среднее значение квадрата разностей (что делает все положительным), а затем извлеките квадратный корень (который отменяет возведение в квадрат). Это называется среднеквадратичной ошибкой (RMSE) или нормой L2 .
важно: забыли свои знания математики ? - это нормально: в этой книге мы обычно предполагаем, что вы закончили математику в средней школе и помните хотя бы часть ее ... Возможно, вы забыли, что такое квадратный корень или как именно с ним работают. Без проблем! Каждый раз, когда вы сталкиваетесь с математической концепцией, которая не объясняется полностью в этой книге, не продолжайте двигаться дальше; вместо этого остановитесь и изучите её. Убедитесь, что вы понимаете основную идею, как она работает и почему мы можем использовать ее. Одно из лучших мест, где можно освежить свои знания, - это Khan Academy. Например, в Khan Academy есть отличное введение в квадратные корни.
Разница между нашей 3 и "идеальной" 3 :
dist_3_abs = (a_3 - mean3).abs().mean()
dist_3_sqr = ((a_3 - mean3)**2).mean().sqrt()
dist_3_abs,dist_3_sqr(tensor(0.1114), tensor(0.2021))
Разница между нашей 3 и "идеальной" 7 :
dist_7_abs = (a_3 - mean7).abs().mean()
dist_7_sqr = ((a_3 - mean7)**2).mean().sqrt()
dist_7_abs,dist_7_sqr(tensor(0.1586), tensor(0.3021))
В обоих случаях расстояние между нашей 3 и «идеальным» 3 меньше, чем расстояние до "идеальной" 7. Так что наша простая модель даст правильный прогноз в этом случае.
PyTorch уже предоставляет обе эти функции в качестве функций потери. Вы найдете их внутри torch.nn.functional, которые команда PyTorch рекомендует импортировать как модуль F (он доступен по умолчанию под этим именем в fastai):
F.l1_loss(a_3.float(),mean7), F.mse_loss(a_3,mean7).sqrt()(tensor(0.1586), tensor(0.3021))
Здесь mse обозначает среднеквадратичную ошибку и l1относится к стандартному математическому жаргону для среднего абсолютного значения (в математике это называется нормой L1 ).
ВАЖНО: Интуитивно разница между нормой L1 и среднеквадратичной ошибкой (MSE) заключается в том, что последняя будет более серьезно наказывать за большие ошибки, чем первая (и будет более снисходительной к мелким ошибкам).
Дж .: Когда я впервые наткнулся на эту штуковину "L1", я посмотрел на нее, чтобы понять, что она означает. Я обнаружил в Google, что это векторная норма, использующая абсолютное значение , поэтому поискал векторную норму и начал читать: Учитывая векторное пространство V над полем F действительных или комплексных чисел, норма на V является любой функцией с неотрицательными значениями. p: V → [0, + ∞) со следующими свойствами: для всех a ∈ F и всех u, v ∈ V, p (u + v) ≤ p (u) + p (v) ...
Затем я остановился. "Ух, я никогда не пойму математику!" - подумал я, в тысячный раз. С тех пор я понял, что каждый раз, когда возникают эти сложные математические фрагменты - на практике, я могу заменить их крошечным фрагментом кода ! Потеря L1 просто равна (a-b).abs().mean(), где a и b- тензоры. Думаю, математики думают иначе, чем я ... В этой книге я позабочусь о том, чтобы каждый раз, когда всплывает какой-нибудь математический жаргон, я дам вам небольшой кусочек кода, которому он равен, и объясню в общем - смысл терминов и что они обозначают.
Мы только что выполнили различные математические операции над тензорами PyTorch. Они похожи на массивы NumPy. Давайте посмотрим на эти две очень важные структуры данных.
Массивы NumPy и тензоры PyTorch
NumPy - это наиболее широко используемая библиотека для научного и числового программирования на Python. Она обеспечивает очень похожую функциональность и очень похожий API на тот, что предоставляется PyTorch; однако он не поддерживает использование графического процессора или вычисление градиентов, которые имеют решающее значение для глубокого обучения. Поэтому в этой книге мы обычно будем использовать тензоры PyTorch вместо массивов NumPy, где это возможно.
(Обратите внимание, что fastai добавляет некоторые функции в NumPy и PyTorch, чтобы сделать их немного более похожими друг на друга. Если какой-либо код в этой книге не работает на вашем компьютере, возможно, вы забыли включить такую строку в начале вашего ноутбука:. from fastai.vision.all import *)
Но что такое массивы и тензоры и почему это должно вас волновать?
Python медленный по сравнению со многими языками. Все, что работает быстро в Python, NumPy или PyTorch, является оберткой скомпилированного объекта, написанного (и оптимизированного) на другом языке, в частности C. Фактически, массивы NumPy и тензоры PyTorch могут производить вычисления во много тысяч раз быстрее, чем при использовании чистого Python.
Массив NumPy - это многомерная таблица данных со всеми элементами одного типа. Поскольку это может быть любой тип, они могут быть даже массивами массивов, причем самые внутренние массивы потенциально могут иметь разные размеры - это называется «зубчатым массивом». Под «многомерной таблицей» мы подразумеваем, например, список (измерение одного), таблицу или матрицу (измерение два), «таблицу таблиц» или «куб» (измерение три) и так далее. Если все элементы имеют какой-то простой тип, такой как integer или float, NumPy сохранит их в памяти как компактную структуру данных C. Вот где сияет NumPy. NumPy имеет широкий спектр операторов и методов, которые могут выполнять вычисления над этими компактными структурами с той же скоростью, что и оптимизированный C, поскольку они написаны на оптимизированном C.
Тензор PyTorch - это почти то же самое, что и массив NumPy, но с дополнительным ограничением, которое открывает некоторые дополнительные возможности. То же самое в том смысле, что это многомерная таблица данных со всеми элементами одного типа. Однако ограничение состоит в том, что тензор не может использовать разный тип данных - он должен использовать один базовый, числовой тип для всех компонентов. Например, тензор PyTorch не может быть зубчатым. Это всегда многомерная прямоугольная структура правильной формы.
Подавляющее большинство методов и операторов, поддерживаемых NumPy для этих структур, также поддерживаются PyTorch, но тензоры PyTorch имеют дополнительные возможности. Одна из основных возможностей заключается в том, что эти структуры могут работать на GPU, и в этом случае их вычисления будут оптимизированы для GPU и могут работать намного быстрее (учитывая большое количество значений для работы). Кроме того, PyTorch может автоматически вычислять производные этих операций, включая комбинации операций. Как вы увидите, без этой возможности было бы невозможно глубокое обучение на практике.
ВАЖНО: Если вы не знаете, что такое C, не волнуйтесь, он вам вообще не понадобится. В двух словах, это низкоуровневый (низкоуровневый означает более похожий на язык, который компьютеры используют внутри) язык, который очень быстр по сравнению с Python. Чтобы воспользоваться преимуществами его скорости при программировании на Python, постарайтесь как можно больше избегать циклов и заменить их командами, которые работают непосредственно с массивами или тензорами.
Возможно, самый важный новый навык программирования, который должен освоить программист Python, - это эффективное использование API массивов / тензоров. Позже в этой книге мы покажем еще много уловок, но вот краткое изложение ключевых вещей, которые вам нужно знать на данный момент.
Чтобы создать массив или тензор, передайте список (или список списков, или список списков списков и т. Д.) В array()или tensor():
data = [[1,2,3],[4,5,6]]
arr = array(data)
tns = tensor(data)arr # numpyarray([[1, 2, 3],
[4, 5, 6]])
tns # pytorchtensor([[1, 2, 3],
[4, 5, 6]])
Все последующие операции показаны на тензорах, но синтаксис и результаты для массивов NumPy идентичны.
Вы можете выбрать строку (обратите внимание, что, как и списки в Python, тензоры индексируются 0, поэтому 1 относится ко второй строке / столбцу):
tns[1]tensor([4, 5, 6])
или столбец, используя : для обозначения всей первой оси (мы иногда называем размеры тензоров / массивов осями ):
tns[:,1]tensor([2, 5])
Вы можете комбинировать их с синтаксисом фрагмента Python ( [start:end] с исключением end), чтобы выбрать часть строки или столбца:
tns[1,1:3]tensor([5, 6])
И вы можете использовать стандартные операторы , такие как +, -, *, /:
tns+1tensor([[2, 3, 4],
[5, 6, 7]])
Тензоры имеют тип:
tns.type()'torch.LongTensor'
И автоматически изменяет тип по мере необходимости, например с int на float:
tns*1.5tensor([[1.5000, 3.0000, 4.5000],
[6.0000, 7.5000, 9.0000]])
Итак, наша базовая модель хороша? Чтобы выразить это количественно, мы должны определить метрику.
Вычисление показателей с помощью широковещания (Computing Metrics Using Broadcasting)
Broadcast (Широковещание) — форма передачи данных, при которой каждый переданный пакет данных достигает всех участников сети одновременно.
Напомним, что метрика - это число, которое рассчитывается на основе прогнозов нашей модели и правильных меток в нашем наборе данных, чтобы показать нам, насколько хороша наша модель. Например, мы могли бы использовать любую из функций, которые мы видели в предыдущем разделе, среднеквадратическую ошибку или среднюю абсолютную ошибку, и взять среднее из них по всему набору данных. Однако ни одно из этих чисел не является понятным для большинства людей; на практике мы обычно используем точность в качестве метрики для классификационных моделей.
Как мы уже обсуждали, мы хотим вычислить нашу метрику на проверочном наборе данных. Это для того, чтобы мы по неосторожности не переборщили - то есть обучили модель хорошо работать только над нашими тренировочными данными. Это не критично для нашей модели основанной на сравнении пикселей,так как у нее нет обученных компонентов. Но все равно мы будем использовать проверочный набор, чтобы следовать обычным практикам глубокова обучения.
Чтобы получить проверочный набор, нам нужно полностью удалить некоторые данные из обучения, чтобы модель вообще не видела их. Как оказалось, создатели MNIST уже сделали это за нас. Вы помните каталог под названием valid ? Вот для чего этот каталог!
Итак, для начала давайте создадим тензоры для наших 3 и 7 из этого каталога. Это тензоры, которые мы будем использовать для вычисления метрики, измеряющей качество нашей модели, в основе которой, измерение расстояния между пикселями:
valid_3_tens = torch.stack([tensor(Image.open(o))
for o in (path/'valid'/'3').ls()])
valid_3_tens = valid_3_tens.float()/255
valid_7_tens = torch.stack([tensor(Image.open(o))
for o in (path/'valid'/'7').ls()])
valid_7_tens = valid_7_tens.float()/255
valid_3_tens.shape,valid_7_tens.shape(torch.Size([1010, 28, 28]), torch.Size([1028, 28, 28]))
Хорошо иметь привычку проверять форму тензоров в ходе кодирования. Здесь мы видим два тензора, один из которых представляет набор проверки цифры 3 из 1010 изображений размером 28 × 28, а другой представляет проверочный набор цифры 7 из 1028 изображений размером 28 × 28.
В конечном итоге мы хотим написать функцию, is_3 которая будет определять, является ли произвольное изображение цифрой 3 или цифрой 7. Функция будет решать к какой из наших двух «идеальных цифр» это изображение ближе. Для этого нужно определить понятие расстояния, то есть функцию, которая вычисляет расстояние между пикселями двух изображений.
Мы можем написать простую функцию, которая вычисляет среднюю абсолютную ошибку, используя выражение, которое мы написали в предыдущем разделе:
python def mnist_distance(a,b): return (a-b).abs().mean((-1,-2)) mnist_distance(a_3, mean3)
Это то же самое значение, которое мы ранее вычислили для расстояния между этими двумя изображениями, идеальным изображением цифры 3 - mean3 и произвольным образцом цифры 3 - a_3, которые оба являются тензорами с формой [28,28].
Но чтобы рассчитать показатель общей точности, нам нужно будет рассчитать расстояние до идеальной цифры 3 для каждого изображения в проверочном наборе. Как мы cделаем это? Мы могли бы написать цикл для всех тензоров одного изображения, которые сложены в нашем тензоре проверочного набора, valid_3_tens с формой [1010,28,28]представляя 1010 изображений. Но есть способ получше.
Что-то очень интересное происходит, когда мы берем ту же самую функцию расстояния, предназначенную для сравнения двух отдельных изображений, но передаем в качестве аргумента тензор valid_3_tens, который представляет проверочный набор цифры 3:
def mnist_distance(a,b): return (a-b).abs().mean((-1,-2))
mnist_distance(a_3, mean3)(tensor([0.1130, 0.1138, 0.1045, ..., 0.1382, 0.1142, 0.1787]), torch.Size([1010]))
Вместо того чтобы жаловаться на несоответствие форм, функция mnist_distance возвращает расстояние для каждого отдельного изображения в виде вектора (т.е. Тензора ранга 1) длиной 1010 (цифры 3-ки в нашем проерочном наборе). Как это случилось?
Взгляните еще раз на нашу функцию mnist_distance, и вы увидите, что у нас есть вычитание (a-b). Волшебный трюк в том, что PyTorch, когда пытается выполнить простую операцию вычитания между двумя тензорами разного ранга, будет использовать широковещательную (Broadcasting) рассылку . То есть он автоматически расширит тензор с меньшим рангом до того же размера, что и тензор с большим рангом. Широковещательная передача (Broadcasting) - важная возможность, которая значительно упрощает написание тензорного кода.
После широковещательной передачи (Broadcasting), чтобы два тензора аргументов имели один и тот же ранг, PyTorch применяет свою обычную логику для двух тензоров одного и того же ранга: он выполняет операцию над каждым соответствующим элементом двух тензоров и возвращает результат тензора. Например:
valid_3_dist = mnist_distance(valid_3_tens, mean3)
valid_3_dist, valid_3_dist.shapetensor([2, 3, 4])
Итак, в этом случае PyTorch обрабатывает mean3 тензор ранга 2, представляющий одно изображение, как если бы это были 1010 копий одного и того же изображения, а затем вычитает каждую из этих копий из каждой цифры 3 в нашем проверочном наборе. Какую форму вы ожидаете от этого тензора? Попытайтесь понять это сами, прежде чем смотреть на ответ ниже:
tensor([1,2,3]) + tensor(1)torch.Size([1010, 28, 28])
Мы вычисляем разницу между нашей «идеальной 3» и каждым изображением из 1010 цифры 3 в нашем проверочном наборе.В результате чего получается форма [1010,28,28].
Есть несколько важных моментов в реализации вещания(Broadcasting), которые делают его ценным не только для выразительности, но и для производительности:
- PyTorch на самом деле не копирует mean3 1010 раз. Он делает вид, что это тензор такой формы, но на самом деле не выделяет никакой дополнительной памяти.
- Он выполняет все вычисления на C (или, если вы используете GPU, в CUDA, эквивалент C на GPU), в десятки тысяч раз быстрее, чем чистый Python (до миллионов раз быстрее на GPU! ).
Это верно для всех широковещательных (Broadcasting) и поэлементных операций и функций, выполняемых в PyTorch. Это самый важный метод создания эффективного кода PyTorch, который вам нужно знать.
Далее в функции mnist_distance мы видим abs. Теперь вы можете догадаться, что это делает в применении к тензору. Он применяет метод к каждому отдельному элементу тензора (применяет метод «поэлементно»). Итак, в этом случае мы вернем 1010 матриц абсолютных значений.
Наконец, наша функция вызывает mean((-1,-2)). Кортеж (-1,-2) представляет собой диапазон осей. В Python -1 относится к последнему элементу, а -2 относится к предпоследнему. В этом случае это говорит PyTorch, что мы хотим взять среднее значение по значениям, индексированным двумя последними осями тензора. Последние две оси - это размеры изображения по горизонтали и вертикали. После взятия среднего по двум последним осям у нас осталась только первая тензорная ось, которая индексирует количество наших изображений, поэтому наш окончательный размер был таким (1010).Другими словами, для каждого изображения мы усредили интенсивность всех пикселей на этом изображении.
В этой книге мы узнаем намного больше о broadcasting, особенно в < >, и будем регулярно практиковать это.
Мы можем использовать, mnist_distance чтобы выяснить, является ли изображение цифрой 3 или нет, используя следующую логику: если расстояние между рассматриваемой цифрой и идеальной 3 меньше, чем расстояние до идеальной 7, то это 3. Эта функция будет автоматически выполняет трансляцию и применяется поэлементно, как и все функции и операторы PyTorch:
def is_3(x): return mnist_distance(x,mean3) < mnist_distance(x,mean7)Давайте проверим это на нашем примере:
is_3(a_3), is_3(a_3).float()(tensor(True), tensor(1.))
Обратите внимание, что когда мы конвертируем логический ответ в число с плавающей точкой, мы получаем 1.0 for True и 0.0 for False. Благодаря трансляции (broadcasting) мы также можем протестировать его на полном проверочном наборе цифры 3:
is_3(valid_3_tens)tensor([ True, True, True, ..., False, True, False])
Теперь мы можем вычислить точность для каждой цифры 3 и цифры 7, взяв среднее значение этой функции для всех 3 и ее обратное значение для всех 7:
accuracy_3s = is_3(valid_3_tens).float() .mean()
accuracy_7s = (1 - is_3(valid_7_tens).float()).mean()
accuracy_3s,accuracy_7s,(accuracy_3s+accuracy_7s)/2(tensor(0.9168), tensor(0.9854), tensor(0.9511))
Похоже, начало неплохое! Мы получаем более 90% точности как для 3, так и для 7, и мы увидели, как удобно определять метрику с помощью широковещательной передачи (broadcasting).
Но давайте будем честными: 3 и 7 - очень разные цифры. И мы пока классифицируем только 2 из 10 возможных цифр (В наборе MNIST 10 цифр от 0 до 9). Так что нам нужно сделать лучше!
Пришло время попробовать систему, которая действительно обучается, то есть может автоматически изменять себя для повышения своей производительности. Другими словами, пора поговорить о тренировочном процессе и SGD.
Стохастический градиентный спуск (SGD)
Вы помните, как Артур Сэмюэл описал машинное обучение, которое мы цитировали в < >?
: Предположим, мы организуем некоторые автоматические средства проверки эффективности любого текущего назначения веса с точки зрения фактической производительности и обеспечиваем механизм для изменения назначения веса, чтобы максимизировать производительность. Нам не нужно вдаваться в подробности такой процедуры, чтобы увидеть, что ее можно сделать полностью автоматической, и чтобы машина, запрограммированная таким образом, «училась» на своем опыте.
Как мы уже говорили, это ключ к созданию модели, которая может становиться все лучше и лучше, может обучаться. Но наш подход схожести пикселей на самом деле этого не делает. У нас нет значения веса или какого-либо способа улучшения, основанного на проверке эффективности веса. Другими словами, мы не можем улучшить наш подход к подобию пикселей, изменив набор параметров. Чтобы воспользоваться преимуществами глубокого обучения, нам сначала нужно представить нашу задачу так, как ее описал Артур Сэмюэл.
Вместо того, чтобы пытаться найти сходство между изображением и «идеальным изображением», мы могли бы вместо этого взглянуть на каждый отдельный пиксель и придумать набор весов для каждого из них, так чтобы самые высокие веса были связаны с теми пикселями, которые, скорее всего, будут черными для определенной категории. Например, пиксели в правом нижнем углу вряд ли будут активированы для 7, поэтому они должны иметь низкий вес для 7, но они, вероятно, будут активированы для 8, поэтому они должны иметь высокий вес для 8. Это может быть представлено как функция и значения весов для каждой возможной категории - например, вероятность быть числом 8:
def pr_eight(x,w): return (x*w).sum()#id gradient_descent
#caption Процесс градиентного спуска
#alt График, показывающий этапы градиентного спуска
gv('''
init->predict->loss->gradient->step->stop
step->predict[label=repeat]
''')Есть много разных способов выполнить каждый из этих семи шагов, и мы будем изучать их на протяжении всей оставшейся части этой книги. Это детали, которые имеют большое значение для практиков глубокого обучения. Общий подход, к каждой из них, следует некоторым основным принципам. Вот несколько рекомендаций:
- Инициализация (Initialize) :: Мы инициализируем параметры случайными значениями. Это может показаться странным. Конечно, есть и другие варианты, которые мы могли бы сделать, например, инициализировать их процентом раз, когда пиксель активируется для этой категории.Но мы знаем, что у нас есть процедура для улучшения и можно начать со случайных весов.
- Потеря (Loss): Это то, что имел в виду Сэмюэл, когда говорил о проверке эффективности любого текущего значения веса с точки зрения фактических результатов . Нам нужна какая-то функция, которая вернет небольшое число, если модель работает хорошо (стандартный подход - рассматривать небольшую потерю как хорошую, а большую потерю как плохую).
- Шаг(Step): Простой способ выяснить, следует ли немного увеличить или уменьшить вес и посмотреть, увеличится или уменьшится потеря. Как только вы найдете правильное направление, вы можете изменить немного больше или меньше, пока не найдете оптимальные веса. Однако это медленно! Как мы увидим, магия исчисления позволяет нам напрямую выяснить, в каком направлении и примерно на сколько изменить каждый вес, без необходимости пробовать все эти небольшие изменения. Это можно сделать путем вычисления градиентов.Это всего лишь оптимизация производительности, мы бы получили точно такие же результаты, если бы использовали более медленный ручной процесс.
- Стоп (Stop): После определенного количества эпох,выбранных нами, обучение останавливается. Для нашего классификатора цифр, мы будем продолжать обучение до тех пор, пока точность модели не станет ухудшаться или у нас не закончится время.
Прежде чем применять эти шаги к нашей задаче классификации изображений, давайте проиллюстрируем, как они выглядят в более простом случае. Сначала мы определим очень простую функцию, квадратичную - давайте представим, что это наша функция потерь и x весовой параметр функции:
def f(x): return x**2Вот график этой функции:
plot_function(f, 'x', 'x**2')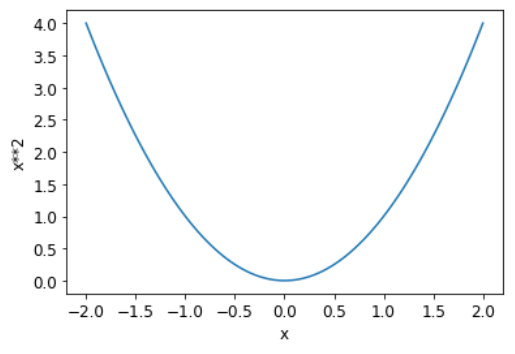
Последовательность шагов, которую мы описали ранее, начинается с выбора некоторого случайного значения для параметра и вычисления значения потерь:
plot_function(f, 'x', 'x**2')
plt.scatter(-1.5, f(-1.5), color='red');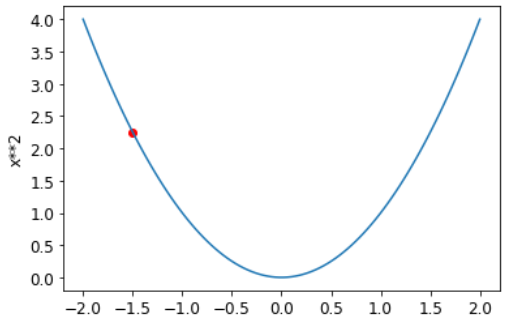
Теперь посмотрим, что произойдет, если мы немного увеличим или уменьшим наш параметр - корректировку . Это просто наклон в определенной точке:
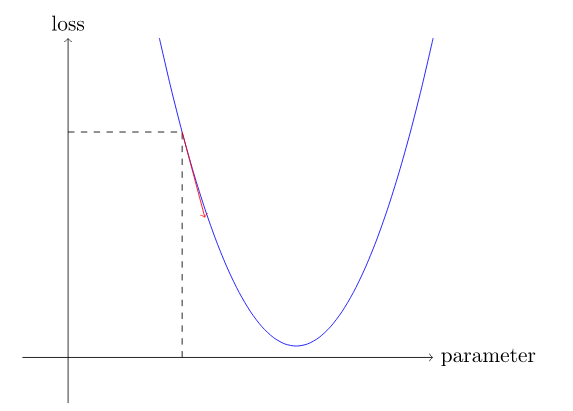
Мы можем немного изменить наш вес в направлении уклона, снова рассчитать наши потери и корректировку и повторить это несколько раз. В конце концов, мы доберемся до самой низкой точки на нашей кривой:
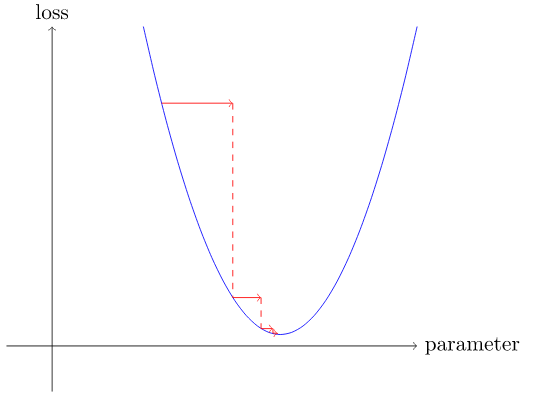
Эта основная идея восходит к Исааку Ньютону, который указал, что таким образом мы можем оптимизировать произвольные функции. Независимо от того, насколько сложными становятся наши функции. Этот базовый подход градиентного спуска существенно не изменится. Единственные незначительные изменения, которые мы увидим позже - это несколько удобных способов сделать это быстрее.
Расчет градиентов
Одним из магических шагов является бит, где мы вычисляем градиенты. Как мы уже упоминали, мы используем исчисление для оптимизации производительности; это позволяет нам более быстро рассчитать, увеличатся или уменьшатся наши потери (loss), когда мы изменим наши параметры вверх или вниз. Градиенты подскажут нам, насколько нужно изменить каждый вес, чтобы сделать модель лучше.
Вы, возможно, помните из своего школьного урока математического анализа, что производная функции говорит вам, насколько изменение ее параметров повлияет на ее результат. Если нет, не волнуйтесь, многие из нас забывают математику, когда школа остается позади! Но вам нужно будет иметь некоторое интуитивное понимание того, что такое производная, прежде чем вы продолжите, поэтому, если все это очень туманно, отправляйтесь в Академию Хана и завершите уроки по основным производным . Вам не нужно знать, как их вычислять самостоятельно, вам просто нужно знать, что такое производная.
Ключевой момент производной заключается в следующем: для любой функции, такой как квадратичная функция, которую мы видели в предыдущем разделе, мы можем вычислить ее производную. Производная - это еще одна функция. Она вычисляет изменение, а не значение. Например, производная квадратичной функции при значении 3 говорит нам, насколько быстро функция изменяется при значении 3. Более конкретно, вы можете вспомнить, что градиент определяется как подъем / спуск, то есть изменение значения функции, деленное на изменение значения параметра. Когда мы знаем, как изменится наша функция, тогда мы знаем, что нам нужно сделать, найти её минимум. Это ключ к машинному обучению: возможность изменять параметры функции, чтобы сделать ее меньше. Исчисление предоставляет нам вычислительную комбинацию, производную, которая позволяет нам непосредственно вычислять градиенты наших функций.
Важно помнить, что у нашей функции много весов, которые нам нужно настроить, поэтому при вычислении производной мы получим не одно число, а их множество - градиент для каждого веса. Но здесь нет ничего математически сложного; вы можете вычислить производную по одному весу и рассматривать все остальные как постоянные, а затем повторить это для каждого другого веса. Вот как рассчитываются все градиенты для каждого веса.
Мы только что упомянули, что вам не придется вычислять градиенты самостоятельно. Как это может быть? Как ни удивительно, PyTorch может автоматически вычислять производную практически любой функции! Более того, он делает это очень быстро. В большинстве случаев она будет не менее быстрой, чем любая производная функция, которую вы можете создать вручную. Посмотрим на пример.
Во-первых, давайте выберем тензорное значение, при котором мы хотим получить градиенты:
xt = tensor(3.).requires_grad_()Обратите внимание на специальный метод requires_grad_ ? Это магическое заклинание, которое мы используем, чтобы сообщить PyTorch, что мы хотим вычислить градиенты относительно этой переменной. По сути, это тегирование переменной, поэтому PyTorch будет помнить о том, чтобы отслеживать, как вычислять градиенты других, прямых вычислений, которые вы запросите.
a: Этот API может сбить вас с толку, если вы пришли из математики или физики. В этих контекстах «градиент» функции - это просто другая функция (т.е. её производная). Но в глубоком обучении «градиенты» обычно означают значение производной функции при определенном значении аргумента. PyTorch API также уделяет внимание аргументу, а не функции, градиенты которой вы фактически вычисляете. Кажется , что должно быть наоборот, но это просто другая перспектива.
Теперь мы вычисляем нашу функцию с этим значением. Обратите внимание, как PyTorch печатает не только вычисленное значение, но и примечание о том, что у него есть функция градиента, которую он будет использовать для вычисления наших градиентов при необходимости:
yt = f(xt)
yttensor(9., grad_fn=<PowBackward0>)
Наконец, мы говорим PyTorch рассчитать за нас градиенты:
yt.backward()«Обратное распространение» здесь относится к обратному распространению ошибки, так называемому процессу вычисления производной каждого слоя. Мы увидим, когда вычислим градиенты глубокой нейронной сети с нуля. Это называется «обратным проходом» сети, в отличие от «прямого прохода», на котором рассчитываются активации. Жизнь, вероятно, была бы проще, если бы backward просто назвали calculate_grad, но люди, занимающиеся глубоким обучением, действительно любят добавлять специфику везде, где они могут!
Теперь мы можем просмотреть градиенты, проверив атрибут grad нашего тензора:
xt.gradtensor(6.)
Если вы помните свои школьные правила исчисления, производная от x**2 равна 2*x, и у нас x=3, поэтому градиенты должны быть такими 2*3=6, что PyTorch и рассчитал для нас!
Теперь мы повторим предыдущие шаги, но с векторным аргументом для нашей функции:
xt = tensor([3.,4.,10.]).requires_grad_()
xttensor([ 3., 4., 10.], requires_grad=True)
И мы добавим sum к нашей функции, чтобы она могла принимать вектор (т.е. Тензор ранга 1) и возвращать скаляр (т.е. Тензор ранга 0):
def f(x): return (x**2).sum()
yt = f(xt)
yttensor(125., grad_fn=<SumBackward0>)
yt.backward()
xt.gradtensor([ 6., 8., 20.])
Наши градиенты 2*xt такие как мы и ожидали!
Градиенты говорят нам только о наклоне нашей функции, но не о том, как именно настроить параметры. Но это дает подсказку; если наклон очень большой, это может означать, что нам нужно сделать больше корректировок, тогда как если наклон очень мал, это может указывать на то, что мы близки к оптимальному значению.
Выбор шага скорости обучения
Решение о том, как изменить наши параметры на основе значений градиентов, является важной частью процесса глубокого обучения. Почти все подходы начинаются с базовой идеи умножения градиента на некоторое небольшое число, называемое скоростью обучения (LR). Скорость обучения часто составляет от 0,001 до 0,1, хотя это может быть что угодно. Часто люди выбирают скорость обучения, просто попробовав несколько значений и найдя лучшее для обучения модели (позже в этой книге мы покажем вам лучший подход, называемый поисковиком скорости обучения ). Выбрав скорость обучения, вы можете настроить параметры с помощью функции:
w -= gradient(w) * lrЭто называется пошаговым изменением параметров с использованием шага оптимизатора .
Если вы выберете слишком низкую скорость обучения, это может означать, что вам придется делать много шагов:
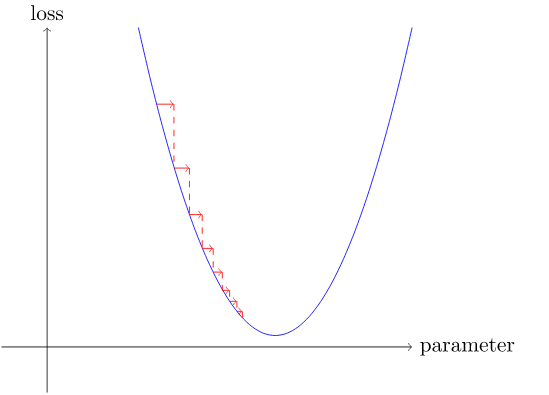
Но хуже выбрать слишком большую скорость обучения , это может привести к увеличению ошибки!
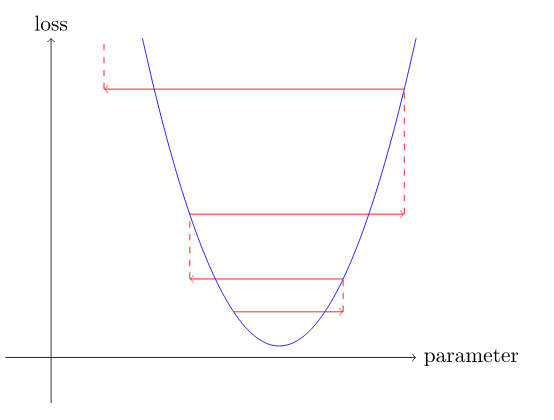
Если скорость обучения слишком высока, она может «подпрыгивать», а не расходиться.
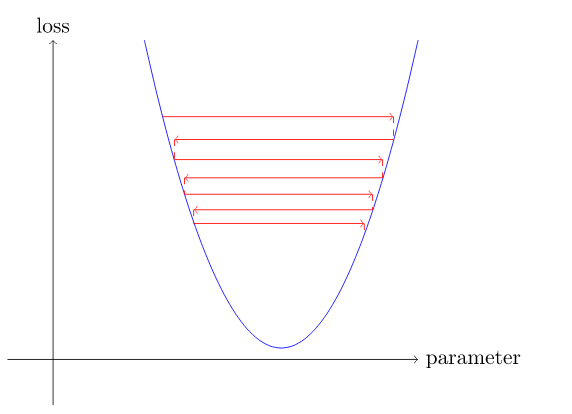
Теперь давайте применим все это в конце концов.
Пример SGD
Мы видели, как использовать градиенты, чтобы найти минимум. Теперь пришло время взглянуть на пример SGD и посмотреть, как найти минимум для обучения модели, чтобы она лучше соответствовала данным.
Начнем с простой синтетической модели. Представьте, что вы измеряете скорость на американских горках. Она быстро увеличивалась, а затем замедлялась по мере подъема на холм. Она меньше всего на вершине, но увеличивается при спуске. Вы хотите построить модель того, как скорость изменяется с течением времени. Если бы вы измеряли скорость вручную каждую секунду в течение 20 секунд, это могло бы выглядеть примерно так:
time = torch.arange(0,20).float(); timetensor([ 0., 1., 2., 3., 4., 5., 6., 7., 8., 9., 10., 11., 12., 13., 14., 15., 16., 17., 18., 19.])
speed = torch.randn(20)*3 + 0.75*(time-9.5)**2 + 1
plt.scatter(time,speed);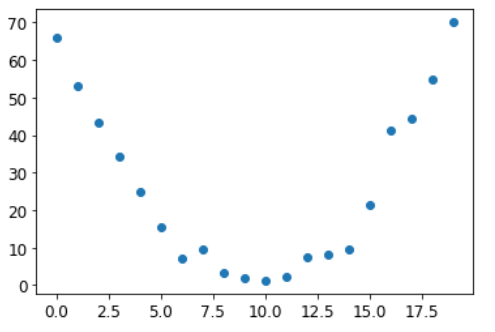
Мы добавили немного случайного шума, так как измерения вручную неточны. Значит, не так-то просто ответить на вопрос: какова была скорость американских горок? Используя SGD, мы можем попытаться найти функцию, которая соответствует нашим наблюдениям. Мы не можем рассмотреть все возможные функции, поэтому предположим, что она будет квадратичной; т.е. функция формы a*(time**2)+(b*time)+c.
Мы хотим четко различать входные данные функции (время, когда мы измеряем скорость) и ее параметры (значения, определяющие, какую квадратичную функцию мы используем). Итак, давайте соберем параметры в одном аргументе и таким образом разделим входные данные t и параметры params в сигнатуре функции:
def f(t, params):
a,b,c = params
return a*(t**2) + (b*t) + cДругими словами, мы ограничили задачу поиска наилучшей вообразимой функции, которая соответствует данным, поиском наилучшей квадратичной функции. Это значительно упрощает задачу, так как каждая квадратичная функция полностью определяется тремя параметрами a, b, и c. Таким образом, чтобы найти лучшую функцию, нам нужно найти лучшие значения a, b и c.
Если мы сможем решить эту проблему для трех параметров квадратичной функции, мы сможем применить тот же подход к другим, более сложным функциям с большим количеством параметров, таким как нейронная сеть. Давайте сначала найдем параметры для f, а затем вернемся и сделаем то же самое с нейронной сетью для набора данных MNIST .
Сначала нам нужно определить, что мы подразумеваем под словом «лучший». Мы определяем это, выбирая функцию потерь , которая будет возвращать значение, основанное на прогнозе и цели, где более низкие значения функции соответствуют «лучшим» прогнозам. Для непрерывных данных обычно используется среднеквадратичная ошибка:
def mse(preds, targets): return ((preds-targets)**2).mean()Теперь давайте проработаем наш 7-шаговый процесс.
Шаг 1: Инициализировать параметры
Сначала мы инициализируем параметры случайными значениями и сообщаем PyTorch, что мы хотим отслеживать их градиенты, используя requires_grad_:
params = torch.randn(3).requires_grad_()#hide
orig_params = params.clone()Шаг 2. Рассчитайте прогнозы
Далее рассчитываем прогнозы:
preds = f(time, params)Давайте создадим небольшую функцию, чтобы увидеть, насколько наши прогнозы близки к нашим целям, и посмотрим:
def show_preds(preds, ax=None):
if ax is None: ax=plt.subplots()[1]
ax.scatter(time, speed)
ax.scatter(time, to_np(preds), color='red')
ax.set_ylim(-300,100)show_preds(preds)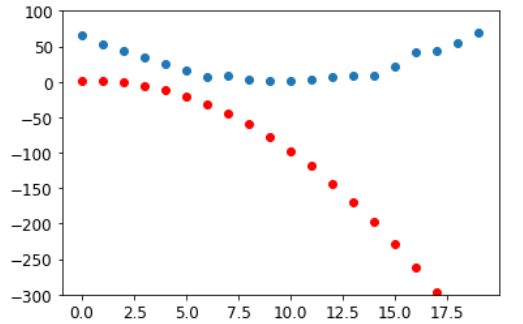
Это выглядит не очень похоже — наши случайные параметры предполагают, что американские горки в конечном итоге будут двигаться назад, так как у нас отрицательные скорости!
Шаг 3: Рассчитайте ошибку
Мы рассчитываем ошибку следующим образом:
loss = mse(preds, speed)
losstensor(38268.9141, grad_fn=<MeanBackward0>)
Наша цель сейчас - улучшить это. Для этого нам нужно знать градиенты.
Шаг 4: Рассчитайте градиенты
Следующим шагом будет расчет градиентов. Другими словами, вычислите примерное изменение параметров:
loss.backward()
params.gradtensor([-65078.6758, -4151.7407, -298.9366])
params.grad * 1e-5tensor([-0.6508, -0.0415, -0.0030])
Мы можем использовать эти градиенты для улучшения наших параметров. Нам нужно будет выбрать скорость обучения (мы обсудим, как это сделать на практике, в следующей главе; пока мы просто будем использовать 1e-5 или 0,00001):
paramstensor([-1.0935, 1.1351, 0.7592], requires_grad=True)
Шаг 5: Шаг весов
Теперь нам нужно обновить параметры на основе только что рассчитанных градиентов:
lr = 1e-5
params.data -= lr * params.grad.data
params.grad = Nonea: Понимание этого зависит от запоминания недавней истории.Чтобы рассчитать градиенты, мы применяем обратное распространение ошибки (backward on the loss). Потеря (loss) была вычислена с помощью функции mse, которой на вход подали параметр preds, который был рассчитан с использованием f , в которой мы первоначально использовали required_grads_. Эта цепочка вызовов функций представляет собой математическую композицию функций, которая позволяет PyTorch использовать правило цепочки исчисления под капотомдля вычисления этих градиентов.
Посмотрим, улучшилась ли потеря:
preds = f(time,params)
mse(preds, speed)tensor(7756.6523, grad_fn=<MeanBackward0>)
И взгляните на график:
show_preds(preds)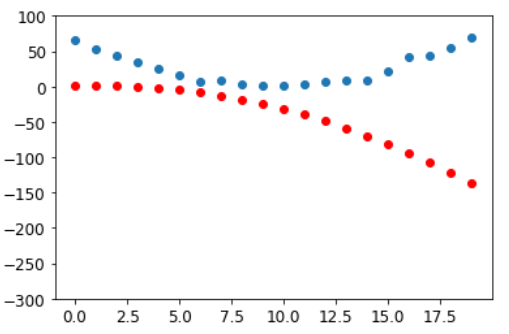
Нам нужно повторить это несколько раз, поэтому мы создадим функцию для применения одного шага:
def apply_step(params, prn=True):
preds = f(time, params)
loss = mse(preds, speed)
loss.backward()
params.data -= lr * params.grad.data
params.grad = None
if prn: print(loss.item())
return predsШаг 6: Повторите процесс
Теперь повторяем. Выполняя цикл и выполняя множество улучшений, мы надеемся достичь хорошего результата:
for i in range(10): apply_step(params)7756.65234375 1982.7974853515625 890.2013549804688 683.4425048828125 644.3111572265625 636.8999633789062 635.4911499023438 635.2183227539062 635.1603393554688 635.1430053710938
#hide
params = orig_params.detach().requires_grad_()Ошибка уменьшается, как мы и надеялись! Глядя только на потери, мы скрываем тот факт, что каждая итерация представляет собой совершенно другую квадратичную функцию, в нашем поиске к нахождению наилучшей из возможных квадратичных функций. Мы можем увидеть этот процесс визуально, если вместо того, чтобы печатать функцию потерь, мы построим график функции на каждом шаге. Тогда мы можем видеть, как форма приближается к наилучшей возможной квадратичной функции для наших данных:
_,axs = plt.subplots(1,4,figsize=(12,3))
for ax in axs: show_preds(apply_step(params, False), ax)
plt.tight_layout()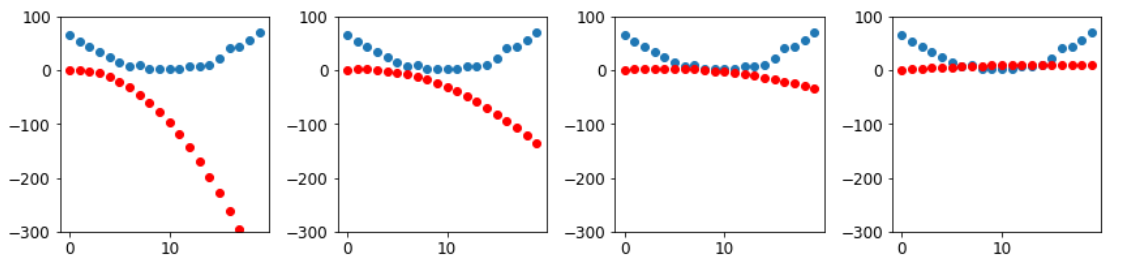
Шаг 7: Стоп
Мы произвольно решили остановиться после 10 эпох обучения. На практике мы бы наблюдали за потерями в обучении и валидации и нашими метриками, чтобы решить, когда остановиться.
Подведение итогов градиентного спуска
#hide_input
#id gradient_descent
#caption The gradient descent process
#alt Graph showing the steps for Gradient Descent
gv('''
init->predict->loss->gradient->step->stop
step->predict[label=repeat]
''')<graphviz.files.Source at 0x7f816e340e80>
Подводя итог, в начале весовые коэффициенты нашей модели могут быть случайными (обучение с нуля) или исходить из заранее обученной модели (трансферное обучение). На первой эпохе обучения, результат, который мы получим, не будет иметь ничего общего с тем, что мы хотим, и вероятно на второй эпохе тоже. Модели нужно обучиться.
Мы сравниваем результы, которые дает нам модель, с нашими целями (мы пометили данные, поэтому мы знаем, какой результат должна дать модель), используя функцию потерь, которая возвращает число, которое мы хотим сделать как можно более меньшим, улучшив наши веса. Для этого мы берем несколько элементов данных (например, изображения) из обучающего набора и передаем их в нашу модель. Мы сравниваем соответствующие цели, используя функцию потерь, и оценки, говорят нам, насколько ошибочны были наши прогнозы. Затем мы немного меняем вес, чтобы сделать его немного лучше.
Для изменения весов, мы используем калькуляцию для расчета градиентов. (На самом деле PyTorch сделает это за нас!) Давайте рассмотрим аналогию. Представьте, что вы заблудились в горах с машиной, припаркованной в самой нижней точке. Чтобы найти путь обратно, вы можете бродить в случайном направлении, но врядли это поможет. Вы знаете, что ваш автомобиль находится в самой низкой точке, и лучше пойти вниз. Всегда делая шаг в направлении самого крутого склона вниз, вы должны в конечном итоге прибыть к месту назначения. Мы используем значение градиента (т.е. крутизну склона), чтобы понять, какой величины шаг сделать; в частности, мы умножаем градиент на число, которое мы выбираем как скорость обучения, чтобы определить размер шага. Мы повторяем это, пока не достигнем низшей точки, которая будет нашей парковкой, тогда мы можем остановиться.
Все, что мы только что видели, можно перенести непосредственно в набор данных MNIST, за исключением функции потерь. Давайте теперь посмотрим, как мы можем определить цель обучения.
Функция потерь MNIST
У нас изображения - это переменные x. Мы объединим их все в один тензор, а также заменим список матриц (тензор ранга 3) на список векторов (тензор ранга 2). Мы сделаем это с помощью метода PyTorch view , который изменяет форму тензора без изменения его содержимого. -1 -это специальный параметр view, который означает «сделайте эту ось настолько большой, насколько это необходимо для размещения всех данных»:
train_x = torch.cat([stacked_threes, stacked_sevens]).view(-1, 28*28)Нам нужна метка для каждого изображения. Мы будем использовать 1 для цифры 3 и 0 для цифры 7:
train_y = tensor([1]*len(threes) + [0]*len(sevens)).unsqueeze(1)
train_x.shape,train_y.shape(torch.Size([12396, 784]), torch.Size([12396, 1]))
Набор данных в PyTorch должен возвращать кортеж (x,y) при индексации. Python предоставляет функцию zip, которая в сочетании со списком обеспечивает простой способ получить эту функциональность:
dset = list(zip(train_x,train_y))
x,y = dset[0]
x.shape,y(torch.Size([784]), tensor([1]))
Для проверочного набора:
valid_x = torch.cat([valid_3_tens, valid_7_tens]).view(-1, 28*28)
valid_y = tensor([1]*len(valid_3_tens) + [0]*len(valid_7_tens)).unsqueeze(1)
valid_dset = list(zip(valid_x,valid_y))Теперь нам нужен (изначально случайный) вес для каждого пикселя (это шаг инициализации в нашем семистадийном процессе):
def init_params(size, std=1.0): return (torch.randn(size)*std).requires_grad_()weights = init_params((28*28,1))Функция weights*pixels не будет достаточно гибкой - она всегда равна 0, если пиксели равны 0 (т.е. ее точка пересечения равна 0). Вы, возможно, помните из школьной математики, что формула для линии y=w*x+b; нам по-прежнему нужна b. Мы инициализируем её случайным числом:
bias = init_params(1)В нейронных сетях w в уравнении y = w * x + b называется весами, а b - уклоном. Вместе веса и уклон составляют параметры.
Параметры: Веса w в уравнении w*x+b, а смещения - b(bias) в этом уравнении.
Теперь мы можем рассчитать прогноз для одного изображения:
(train_x[0]*weights.T).sum() + biastensor([20.2336], grad_fn=<AddBackward0>)
Хотя мы могли бы использовать цикл Python for для вычисления прогноза для каждого изображения, это было бы очень медленно. Поскольку циклы Python не работают на графическом процессоре и поскольку Python является медленным языком для циклов в целом, нам нужно представить как можно больше вычислений в модели, используя функции более высокого уровня.
В этом случае существует чрезвычайно удобная математическая операция, которая вычисляет w*x для каждой строки матрицы — это называется матричным умножением. <> показывает, как выглядит матричное умножение.
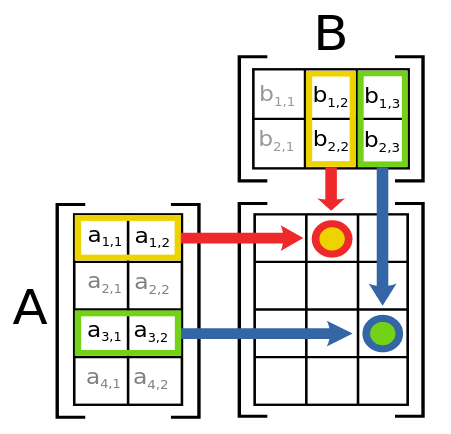
Это изображение показывает две матрицы A и B, умноженные вместе. Каждый элемент результата, который мы назовем AB, содержит каждый элемент соответствующей строки Aумноженный на каждый элемент соответствующего столбца B, сложенный вместе. Например, строка 1, столбец 2 (оранжевая точка с красной рамкой) рассчитывается как $a_{1,1} * b_{1,2} + a_{1,2} * b_{2,2}$. Если вам нужно освежить в памяти умножение матриц, мы предлагаем вам взглянуть на Введение в умножение матриц в Khan Academy , поскольку это самая важная математическая операция в глубоком обучении.
В Python умножение матриц представлено @ оператором. Давай попробуем:
def linear1(xb): return xb@weights + bias
preds = linear1(train_x)
predstensor([[20.2336],
[17.0644],
[15.2384],
...,
[18.3804],
[23.8567],
[28.6816]], grad_fn=<AddBackward0>)
Первый элемент такой же, как мы рассчитали ранее, как и следовало ожидать. Это уравнение batch@weights + bias является одним из двух фундаментальных уравнений любой нейронной сети (второе - это функция активации activation function, которую мы вскоре увидим).
Давайте проверим нашу точность(accuracy). Чтобы решить, представляет ли результат 3 или 7, мы можем просто проверить, превышает ли он 0,5, поэтому наша точность для каждого элемента может быть вычислена (с помощью широковещательной передачи broadcasting, и никаких циклов!):
corrects = (preds>0.5).float() == train_y
correctstensor([[ True],
[ True],
[ True],
...,
[False],
[False],
[False]])
corrects.float().mean().item()0.49080348014831543
Теперь посмотрим, как изменится точность при небольшом изменении одного из весов:
weights[0] *= 1.0001preds = linear1(train_x)
((preds>0.0).float() == train_y).float().mean().item()0.4912068545818329
Как мы видели, нам нужны градиенты, чтобы улучшить нашу модель с помощью SGD, и для расчета градиентов нам нужна некоторая функция потерь, которая представляет, насколько хороша наша модель. Это потому, что градиенты являются мерой того, как эта функция потерь изменяется с небольшими сдвигами весов.
Итак, нам нужно выбрать функцию потерь. Очевидным подходом было бы использование точности, которая является нашей метрикой, как и наша функция потерь. В этом случае мы рассчитываем наш прогноз для каждого изображения, собираем эти значения для расчета общей точности, а затем вычисляем градиенты каждого веса относительно этой общей точности.
К сожалению, у нас здесь значительная техническая проблема. Градиент функции - это ее наклон, или крутизна, которая может быть определена как подъем - то есть, насколько значение функции идет вверх или вниз, деленное на то, насколько мы изменили входные данные. Мы можем написать это как: (y_new - y_old )/( x_new - x_old). Это дает нам хорошее приближение градиента, когда x_new очень похож на x_old, что означает, что их разница очень мала. Но точность меняется только при изменении прогноза с 3 на 7 или наоборот. Проблема в том, что небольшое изменение весов от x_old до x_new вряд ли вызовет изменение какого-либо прогноза, поэтому (y_new - y_old) почти всегда будет равно 0. Другими словами, градиент равен 0 почти везде.
Очень небольшое изменение значения веса часто фактически не изменит точность вообще. Это означает, что бесполезно использовать точность в качестве функции потерь - если мы это сделаем, то большую часть времени наши градиенты будут фактически равны 0, и модель не сможет обучаться.
S: В математических терминах точность - функция, которая постоянна почти везде (кроме порога, 0,5), поэтому её производная равна нулю почти везде (до бесконечности). Это дает градиенты, которые равны 0 или бесконечны и бесполезны для обновления модели.
Вместо этого нам нужна функция потерь, которая, когда наши веса дают немного лучшие прогнозы, дает нам немного лучшие потери. Так как же в точности выглядит «немного лучший прогноз»? Что ж, в этом случае это означает, что если правильный ответ - 3, оценка немного выше, или если правильный ответ - 7, оценка немного ниже.
Напишем сейчас такую функцию. В какой форме?
Функция потерь получает не сами изображения, а прогнозы модели. Давайте сделаем один аргумент prds из значений от 0 до 1, где каждое значение является предсказанием того, что изображение является 3. Это вектор (Тензор ранга 1), индексированный по изображениям.
Цель функции потерь - измерить разницу между прогнозируемыми значениями и истинными значениями, то есть целевыми значениями (также известными как метки). Давайте сделаем еще один аргумент, trgts со значениями 0 или 1, который сообщает, действительно ли изображение равно 3 или нет. Это также вектор (Другой тензор ранга 1), индексированный по изображениям.
Так, например, предположим, что у нас есть три изображения, которые, как мы знаем, являются 3, 7 и 3. И предположим, что наша модель предсказала с высокой степенью уверенности (0,9), что первая была 3, что вторая была 7, с небольшой степенью достоверности (0,4), и с достаточной степенью достоверности (0,2), но неверно, что последняя была 7. Это означало бы, что наша функция потерь получит эти значения в качестве входных данных:
trgts = tensor([1,0,1])
prds = tensor([0.9, 0.4, 0.2])Вот первая попытка функции потерь, которая измеряет расстояние между прогнозами и целями (predictions и targets):
def mnist_loss(predictions, targets):
return torch.where(targets==1, 1-predictions, predictions).mean()Мы используем новую функцию torch.where(a,b,c). Это то же самое, что и запуск списка [b[i] if a[i] else c[i] for i in range(len(a))], за исключением того, что он работает с тензорами на скорости C / CUDA. Говоря простым языком, эта функция будет измерять, насколько далек каждый прогноз от 1, если он должен быть 1, и насколько он удален от 0, если он должен быть 0, а затем будет принимать среднее значение всех этих расстояний.
примечание: прочтите документацию: важно знать о таких функциях PyTorch, как эта, потому что цикл по тензорам в Python выполняется со скоростью Python, а не со скоростью C / CUDA! Попробуйте запустить help(torch.where) сейчас, чтобы прочитать документацию по этой функции, или, что еще лучше, поищите ее на сайте документации PyTorch.
Попробуем на нашем prds и trgts:
torch.where(trgts==1, 1-prds, prds)tensor([0.1000, 0.4000, 0.8000])
Вы можете видеть, что эта функция возвращает меньшее число, когда прогнозы более точны, когда прогнозы более надежны (абсолютные значения больше) и когда неточные прогнозы менее надежны. В PyTorch мы всегда предполагаем, что меньшее значение функции потерь лучше. Поскольку нам нужен скаляр для окончательных потерь, mnist_loss принимает среднее значение предыдущего тензора:
mnist_loss(prds,trgts)tensor(0.4333)
Например, если мы изменим наш прогноз для одной «ложной» цели с 0,2 до 0,8, потери снизятся, что указывает на то, что это лучший прогноз:
mnist_loss(tensor([0.9, 0.4, 0.8]),trgts)tensor(0.2333)
Одна из проблем с mnist_loss в том виде, как она определена в настоящее время, заключается в том, что она предполагает, что прогнозы всегда находятся между 0 и 1. Мы должны убедиться, что это на самом деле так! Есть функция, которая делает именно это - давайте посмотрим.
Сигмоида
sigmoid Функция всегда выдает число между 0 и 1. Это определяется следующим образом :
def sigmoid(x): return 1/(1+torch.exp(-x))Pytorch определяет для нас свою версию, поэтому нам не нужна собственная. Это важная функция в глубоком обучении, поскольку мы часто хотим убедиться, что значения находятся в диапазоне от 0 до 1. Вот как это выглядит:
plot_function(torch.sigmoid, title='Sigmoid', min=-4, max=4)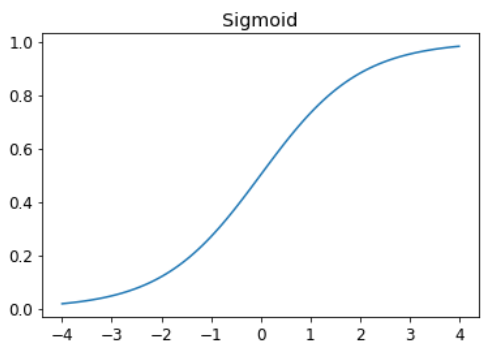
Как видно, он принимает любое входное значение, положительное или отрицательное, и сглаживает его на выходное значение от 0 до 1. Это также гладкая кривая, которая идет только вверх, что облегчает для SGD поиск значимых градиентов.
Давайте обновим mnist_loss, чтобы сначала применить сигмоид к входам:
def mnist_loss(predictions, targets):
predictions = predictions.sigmoid()
return torch.where(targets==1, 1-predictions, predictions).mean()Теперь мы можем быть уверены, что наша функция потерь будет работать, даже если прогнозы не находятся между 0 и 1. Все, что требуется, это то, что большее число предсказания соответствует более высокой достоверности изображения цифры 3.
Определив функцию потерь, сейчас удачный момент, чтобы резюмировать, почему мы это сделали. Ведь у нас уже была метрика, которая была общей точностью. Так почему мы определили потерю?
Ключевое отличие в том, что метрика нужна, чтобы стимулировать понимание человеком, а потеря - в том, чтобы управлять автоматическим обучением. Для этого потеря должна быть функцией, которая имеет значимую производную. Она не может иметь большие плоские участки и большие прыжки, но вместо этого должна быть достаточно гладкой. Вот почему мы разработали функцию потерь, которая будет реагировать на небольшие изменения уровня достоверности. Это требование представляет собой компромисс между нашей реальной целью и функцией, которая может быть оптимизирована с помощью её градиента. Функция потерь вычисляется для каждого элемента в нашем наборе данных, а затем, в конце эпохи, все значения потерь усредняются, и общее среднее значение сообщается для эпохи.
С другой стороны, метрики - это цифры, которые нас действительно волнуют. Это значения, которые печатаются в конце каждой эпохи, которые говорят нам, как на самом деле работает наша модель. Важно, чтобы мы научились фокусироваться на этих метриках, а не на потерях, при оценке качества модели.
SGD и мини-партии (Mini-Batches)
Теперь, когда у нас есть функция потерь, которая подходит для управления SGD, мы можем рассмотреть некоторые детали, задействованные на следующем этапе процесса обучения, который заключается в изменении или обновлении весов на основе градиентов. Это называется этапом оптимизации .
Чтобы сделать шаг оптимизации, необходимо рассчитать потери по одному или нескольким элементам данных. Мы могли бы рассчитать его для всего набора данных и взять среднее значение, или мы могли бы рассчитать его для одного элемента данных. Но ни один из них не идеален. Расчет этого для всего набора данных займет очень много времени.Вычисление его для одного элемента не будет использовать много информации, поэтому это приведет к очень неточному и нестабильному градиенту. То есть вы столкнетесь с проблемой обновления весов.
Поэтому вместо этого мы идем на компромис между ними: мы вычисляем среднюю потерю для нескольких элементов данных одновременно. Это называется мини-партия . Количество элементов данных в мини-пакете называется размером пакета . Больший размер пакета означает, что вы получите более точную и стабильную оценку градиентов вашего набора данных с помощью функции потерь, но это займет больше времени, и вы будете обрабатывать меньше мини-пакетов за эпоху. Выбор подходящего размера пакета - одно из решений, которые вам необходимо принять как специалисту по глубокому обучению, чтобы быстро и точно обучить свою модель. О том, как сделать этот выбор, мы будем говорить на протяжении всей этой книги.
Еще одна веская причина для использования мини-пакетов вместо расчета градиента для отдельных элементов данных заключается в том, что на практике мы почти всегда проводим обучение на ускорителе, таком как графический процессор. Эти ускорители работают хорошо только в том случае, если у них есть много работы за раз, поэтому будет полезно, если мы сможем дать им много элементов данных для работы. Использование мини-пакетов - один из лучших способов сделать это. Однако, если вы дадите им слишком много данных для одновременной работы, у них закончится память - сделать GPU счастливыми тоже сложно!
Как мы видели при обсуждении увеличения данных в < >, мы получим лучшее обобщение, если сможем варьировать элементы во время обучения. Одна простая и эффективная идея, состоит в том, какие элементы данных мы помещаем в каждый мини-пакет. Вместо того, чтобы просто перечислять наш набор данных по порядку для каждой эпохи, мы обычно делаем это случайным образом перемешиваем его каждую эпоху, прежде чем создавать мини-пакеты. PyTorch и fastai предоставляют класс, который будет выполнять перетасовку и сортировку мини-пакетов за вас, называемый DataLoader.
A DataLoaderможет взять любую коллекцию Python и превратить ее в итератор для многих пакетов, например:
coll = range(15)
dl = DataLoader(coll, batch_size=5, shuffle=True)
list(dl)[tensor([ 0, 2, 10, 13, 8]), tensor([11, 12, 4, 1, 5]), tensor([ 3, 14, 6, 9, 7])]
Для обучения модели нам нужна не просто коллекция Python, а коллекция, содержащая независимые и зависимые переменные (то есть входные данные и цели модели). Коллекция, содержащая кортежи независимых и зависимых переменных, известна в PyTorch как Dataset. Вот пример очень простого Dataset:
ds = L(enumerate(string.ascii_lowercase))
dsКогда мы передаем Dataset в DataLoader мы получим обратно множество пакетов, которые сами по себе являются кортежами тензоров, представляющих пакеты независимых и зависимых переменных:
dl = DataLoader(ds, batch_size=6, shuffle=True)
list(dl)[(tensor([ 5, 9, 8, 15, 4, 24]), ('f', 'j', 'i', 'p', 'e', 'y')),
(tensor([ 0, 18, 12, 10, 6, 20]), ('a', 's', 'm', 'k', 'g', 'u')),
(tensor([17, 16, 23, 13, 3, 14]), ('r', 'q', 'x', 'n', 'd', 'o')),
(tensor([21, 22, 7, 19, 1, 2]), ('v', 'w', 'h', 't', 'b', 'c')),
(tensor([11, 25]), ('l', 'z'))]
Теперь мы готовы написать наш первый цикл обучения для модели с использованием SGD!
Собираем все вместе
Пришло время реализовать процесс, который мы видели в < >. В коде наш процесс будет реализован примерно так для каждой эпохи:
for x,y in dl:
pred = model(x)
loss = loss_func(pred, y)
loss.backward()
parameters -= parameters.grad * lr
Во-первых, давайте повторно инициализируем наши параметры:
weights = init_params((28*28,1))
bias = init_params(1)A DataLoader может быть создан из Dataset:
dl = DataLoader(dset, batch_size=256)
xb,yb = first(dl)
xb.shape,yb.shape(torch.Size([256, 784]), torch.Size([256, 1]))
Мы сделаем то же самое для набора проверки:
valid_dl = DataLoader(valid_dset, batch_size=256)Создадим для тестирования мини-партию размером 4:
batch = train_x[:4]
batch.shapetorch.Size([4, 784])
preds = linear1(batch)
predstensor([[-2.2569],
[-9.8264],
[-0.1188],
[-6.4979]], grad_fn=<AddBackward0>)
loss = mnist_loss(preds, train_y[:4])
losstensor(0.8583, grad_fn=<MeanBackward0>)
Теперь мы можем рассчитать градиенты:
loss.backward()
weights.grad.shape,weights.grad.mean(),bias.grad(torch.Size([784, 1]), tensor(-0.0121), tensor([-0.0841]))
Давайте поместим все это в функцию:
def calc_grad(xb, yb, model):
preds = model(xb)
loss = mnist_loss(preds, yb)
loss.backward()и протестируем:
calc_grad(batch, train_y[:4], linear1)
weights.grad.mean(),bias.grad(tensor(-0.0362), tensor([-0.2523]))
Но посмотрите, что произойдет, если мы вызовем его дважды:
calc_grad(batch, train_y[:4], linear1)
weights.grad.mean(),bias.grad(tensor(-0.0241), tensor([-0.1682]))
Градиенты изменились! Причина этого в том, что loss.backwardфактически добавляет градиенты потерь(loss) к любым градиентам, которые хранятся в данный момент. Итак, сначала мы должны установить текущие градиенты на 0:
weights.grad.zero_()
bias.grad.zero_();примечание: Операции на месте: Методы в PyTorch, имена которых заканчиваются подчеркиванием, изменяют свои объекты на месте . Например, bias.zero_() устанавливает все элементы тензора bias в 0.
Наш единственный оставшийся шаг - обновить веса и смещения на основе градиента и скорости обучения. Когда мы это делаем, мы должны сказать PyTorch, чтобы он не брал градиент этого шага - иначе все станет очень запутанным, когда мы попытаемся вычислить производную в следующей партии! Если присвоить атрибуту данных тензора, PyTorch не примет градиент этого шага. Вот наш базовый учебный цикл для эпохи:
def train_epoch(model, lr, params):
for xb,yb in dl:
calc_grad(xb, yb, model)
for p in params:
p.data -= p.grad*lr
p.grad.zero_()Мы также хотим проверить, как у нас дела, посмотрев на точность проверочного набора. Чтобы решить, представляет ли результат 3 или 7, мы можем просто проверить, больше ли он 0. Итак, нашу точность для каждого элемента можно рассчитать (используя broadcasting, поэтому никаких циклов!) С помощью:
(preds>0.0).float() == train_y[:4]tensor([[False],
[False],
[False],
[False]])
Это дает нам функцию для расчета точности:
def batch_accuracy(xb, yb):
preds = xb.sigmoid()
correct = (preds>0.5) == yb
return correct.float().mean()Можем проверить, как она работает:
batch_accuracy(linear1(batch), train_y[:4])tensor(0.)
а затем соедините партии:
def validate_epoch(model):
accs = [batch_accuracy(model(xb), yb) for xb,yb in valid_dl]
return round(torch.stack(accs).mean().item(), 4)validate_epoch(linear1)0.6615
Это наша отправная точка. Давайте потренируемся в течение одной эпохи и посмотрим, улучшится ли точность:
lr = 1.
params = weights,bias
train_epoch(linear1, lr, params)
validate_epoch(linear1)0.7469
Затем сделайте еще несколько:
for i in range(20):
train_epoch(linear1, lr, params)
print(validate_epoch(linear1), end=' ')0.8656 0.9085 0.9251 0.9383 0.9461 0.9529 0.9574 0.9608 0.9618 0.9652 0.9652 0.9666 0.9681 0.9681 0.9686 0.9691 0.9696 0.9701 0.9701 0.9701
Прекрасно выглядит! Мы уже достигли той же точности, что и наш подход «сходства пикселей», и мы создали универсальную основу, на которой мы можем опираться. Нашим следующим шагом будет создание объекта, который будет обрабатывать шаг SGD за нас. В PyTorch это называется оптимизатором.
Создание оптимизатора
Поскольку это основа, PyTorch предоставляет несколько полезных классов, упрощающих реализацию. Первое, что мы можем сделать, это заменить нашу функцию linear1 модулем PyTorch nn.Linear. Модуль является объектом класса , который наследует от класса PyTorch -nn.Module . Объекты этого класса ведут себя идентично стандартным функциям Python - вы можете вызывать их, используя круглые скобки, и они будут возвращать активации модели.
nn.Linear делает то же самое, что и наши init_params и linearвместе взятые. Он содержит как веса, так и смещения в одном классе. Вот как мы воспроизводим нашу модель из предыдущего раздела:
linear_model = nn.Linear(28*28,1)Каждый модуль PyTorch знает, какие параметры у него есть; они доступны через метод parameters :
w,b = linear_model.parameters()
w.shape,b.shape(torch.Size([1, 784]), torch.Size([1]))
Мы можем использовать эту информацию для создания оптимизатора:
class BasicOptim:
def __init__(self,params,lr): self.params,self.lr = list(params),lr
def step(self, *args, **kwargs):
for p in self.params: p.data -= p.grad.data * self.lr
def zero_grad(self, *args, **kwargs):
for p in self.params: p.grad = NoneМы можем создать наш оптимизатор, передав параметры модели:
opt = BasicOptim(linear_model.parameters(), lr)Наш цикл обучения теперь можно упростить до:
def train_epoch(model):
for xb,yb in dl:
calc_grad(xb, yb, model)
opt.step()
opt.zero_grad()Наша функция проверки вообще не нуждается в изменении:
validate_epoch(linear_model)0.5411
Давайте поместим наш небольшой обучающий цикл в функцию, чтобы упростить задачу:
def train_model(model, epochs):
for i in range(epochs):
train_epoch(model)
print(validate_epoch(model), end=' ')Результаты такие же, как и в предыдущем разделе:
train_model(linear_model, 20)0.4932 0.7744 0.854 0.9165 0.936 0.9482 0.956 0.9633 0.9658 0.9667 0.9682 0.9711 0.9726 0.9745 0.9755 0.9765 0.9775 0.978 0.9785 0.9785
fastai предоставляет SGD класс, который по умолчанию делает то же самое, что и наш BasicOptim:
linear_model = nn.Linear(28*28,1)
opt = SGD(linear_model.parameters(), lr)
train_model(linear_model, 20)0.4932 0.8549 0.8359 0.9111 0.9321 0.9462 0.955 0.9628 0.9658 0.9667 0.9692 0.9711 0.9731 0.9745 0.976 0.977 0.9775 0.9775 0.978 0.9789
fastai также предоставляет Learner.fit, который мы можем использовать вместо train_model. Чтобы создать, Learner нам сначала нужно создать DataLoaders, передав наши обучение и проверку DataLoader:
dls = DataLoaders(dl, valid_dl)Чтобы создать объект Learner без использования приложения (например, cnn_learner), мы должны передать все элементы, созданные в этой главе: DataLoaders, модель, функцию оптимизации (которой будут переданы параметры), функцию потери и, при необходимости, любые метрики для печати:
learn = Learner(dls, nn.Linear(28*28,1), opt_func=SGD,
loss_func=mnist_loss, metrics=batch_accuracy)Теперь мы можем вызвать fit:
learn.fit(10, lr=lr)| epoch | train_loss | valid_loss | batch_accuracy | time |
|---|---|---|---|---|
| 0 | 0.636325 | 0.503246 | 0.495584 | 00:00 |
| 1 | 0.451432 | 0.236693 | 0.789500 | 00:00 |
| 2 | 0.168857 | 0.159305 | 0.858685 | 00:00 |
| 3 | 0.075659 | 0.099148 | 0.916585 | 00:00 |
| 4 | 0.041181 | 0.073948 | 0.936703 | 00:00 |
| 5 | 0.027617 | 0.059897 | 0.950442 | 00:00 |
| 6 | 0.021996 | 0.051021 | 0.956330 | 00:00 |
| 7 | 0.019468 | 0.045069 | 0.963199 | 00:00 |
| 8 | 0.018165 | 0.040868 | 0.965653 | 00:00 |
| 9 | 0.017368 | 0.037766 | 0.968106 | 00:00 |
Как видите, в классах PyTorch и fastai нет ничего волшебного. Они просто удобные. Предварительно упакованные части кода, которые делают вашу жизнь немного проще! (Они также предоставляют много дополнительных функций, которые мы будем использовать в будущих главах.)
Этими классами мы теперь можем заменить нашу линейную модель нейронной сетью.
Добавление нелинейности
Пока что у нас есть общая процедура оптимизации параметров функции, и мы опробовали ее на очень скучной функции: простом линейном классификаторе. Линейный классификатор очень ограничен в том, что он может делать. Чтобы сделать его немного более сложным (и способным обрабатывать больше задач), нам нужно добавить что-то нелинейное между двумя линейными классификаторами - это то, что дает нам нейронную сеть.
Вот полное определение базовой нейронной сети:
def simple_net(xb):
res = xb@w1 + b1
res = res.max(tensor(0.0))
res = res@w2 + b2
return resВот и все! Все, что у нас есть, simple_net- это два линейных классификатора с maxфункцией между ними.
Здесь w1 и w2- тензоры весов, b1 и b2- тензоры смещения; то есть параметры, которые изначально инициализируются случайным образом, как и в предыдущем разделе: Именно! Все, что у нас есть в simple_net, это два линейных классификатора с функцией взятия максимума (max) между ними.
Здесь w1 и w2 являются тензорами веса, и b1 и b2 являются тензорами уклона; то есть параметры, которые изначально инициализированы случайным образом, как и в предыдущем разделе:
w1 = init_params((28*28,30))
b1 = init_params(30)
w2 = init_params((30,1))
b2 = init_params(1)Ключевым пунктом является то, что w1 имеет 30 выходных активаций (что означает, что w2 должна иметь 30 входных активаций, чтобы они совпадали). Это означает, что первый слой может создавать 30 различных признаков, каждый из которых представляет собой различное сочетание пикселей. Вы можете изменить это 30 на что угодно, чтобы сделать модель более или менее сложной.
Эта небольшая функция res.max(tensor(0.0)) называется выпрямленной линейной единицей, также известной как ReLU.Думаем, что все согласны с тем, что выпрямленная линейная единица звучит довольно модно и сложно... Но на самом деле в этом нет ничего, кроме res.max(tensor(0.0))- другими словами,- заменить каждое отрицательное число на ноль. Эта крошечная функция также доступна в PyTorch как F.relu:
plot_function(F.relu)
J: В глубоком обучении существует огромное количество жаргона, включая термины, такие как выпрямленная линейная единица. Подавляющее большинство этой терминологии не сложнее, чем может быть реализовано в короткой строке кода, как мы видели в этом примере. Реальность такова, что для того, чтобы ученые опубликовали свои статьи, они должны сделать их как можно более впечатляющими и изощренными. Один из способов сделать это - ввести жаргон. К сожалению, это приводит к тому, что глубокое обучение становится гораздо более устрашающим и труднодоступным, чем должно быть. Вам действительно стоит знать терминологию, потому что в противном случае статьи и учебные пособия будут для вас непонятны. Но это не значит, что терминология должна вас пугать. Помните, что когда вы встречаете слово или фразу, которых раньше не видели, они почти наверняка относятся к очень простой концепции.
Основная идея состоит в том, что, используя больше линейных слоев, мы можем заставить нашу модель выполнять больше вычислений и, следовательно, моделировать более сложные функции. Но нет смысла просто ставить один линейный слой непосредственно за другим, потому что когда мы умножаем элементы вместе, а затем складываем их несколько раз, это может быть заменено умножением и сложением их всего один раз! То есть последовательность из любого числа линейных слоев в одном ряду может быть заменена одним линейным слоем с другим набором параметров.
Но если мы поместим между ними нелинейную функцию, например max, тогда это уже неверно. Теперь каждый линейный слой фактически несколько отделен от других и может выполнять свою полезную работу. Функция maxособенно интересна тем , что она работает как простое ifзаявление.
S: Математически, мы говорим, что композиция двух линейных функций является другой линейной функцией. Таким образом, мы можем сложить столько линейных классификаторов, сколько мы хотим друг с другом.Без нелинейных функций между слоями, он будет просто как один линейный классификатор.
Достаточно удивительно, но математически доказано, что эта маленькая функция может решить любую вычисляемую задачу до произвольно высокого уровня точности, если вы можете найти правильные параметры для w1 и w2 и если вы сделаете эти матрицы достаточно большими. Для любой произвольно волнистой функции мы можем аппроксимировать ее как связку линий, соединенных вместе; чтобы сделать ее ближе к волнистой функции, мы просто должны использовать более короткие линии. Это известно как универсальная теорема аппроксимации. Три строки кода, которые мы имеем здесь, известны как слои. Первый и третий известны как линейные слои, а вторая строка кода известна по-разному как функция нелинейности или активации.
Как и в предыдущем разделе, мы можем заменить этот код чем-то немного проще, воспользовавшись преимуществами PyTorch:
simple_net = nn.Sequential(
nn.Linear(28*28,30),
nn.ReLU(),
nn.Linear(30,1)
)nn.Sequential создает модуль, который по очереди будет вызывать каждый из перечисленных слоев или функций.
nn.ReLU это модуль PyTorch, который выполняет то же самое, что и F.relu функция. Большинство функций, которые могут появляться в модели, также имеют идентичные формы, являющиеся модулями. Как правило, это просто замена F на nn и изменения прописных на строчные буквы. При использовании nn.Sequential PyTorch требует от нас использования версии модуля. Так как модули являются классами, мы должны создать их экземпляры, поэтому в этом примере вы видите nn.ReLU ().
Поскольку nn.Sequential является модулем, мы можем получить его параметры, которые вернут список всех параметров всех модулей, которые он содержит. Давайте попробуем! Поскольку это более сложная модель, мы будем использовать более низкий уровень обучения и еще несколько эпох.
learn = Learner(dls, simple_net, opt_func=SGD,
loss_func=mnist_loss, metrics=batch_accuracy)#hide_output
learn.fit(40, 0.1)| epoch | train_loss | valid_loss | batch_accuracy | time |
|---|---|---|---|---|
| 0 | 0.334253 | 0.400692 | 0.507851 | 00:00 |
| 1 | 0.152872 | 0.234682 | 0.800294 | 00:00 |
| 2 | 0.083949 | 0.117399 | 0.914622 | 00:00 |
| 3 | 0.054701 | 0.079000 | 0.938665 | 00:00 |
| 4 | 0.041214 | 0.061599 | 0.953876 | 00:00 |
| 5 | 0.034378 | 0.051806 | 0.962709 | 00:00 |
| 6 | 0.030487 | 0.045610 | 0.965162 | 00:01 |
| 7 | 0.027977 | 0.041380 | 0.966634 | 00:00 |
| 8 | 0.026177 | 0.038315 | 0.969578 | 00:00 |
| 9 | 0.024787 | 0.035977 | 0.969087 | 00:00 |
| 10 | 0.023658 | 0.034132 | 0.972031 | 00:00 |
| 11 | 0.022715 | 0.032626 | 0.972522 | 00:00 |
| 12 | 0.021910 | 0.031364 | 0.974485 | 00:00 |
| 13 | 0.021211 | 0.030284 | 0.975466 | 00:00 |
| 14 | 0.020596 | 0.029346 | 0.975466 | 00:00 |
| 15 | 0.020050 | 0.028519 | 0.975957 | 00:00 |
| 16 | 0.019561 | 0.027783 | 0.976448 | 00:00 |
| 17 | 0.019119 | 0.027123 | 0.977429 | 00:00 |
| 18 | 0.018717 | 0.026528 | 0.977429 | 00:00 |
| 19 | 0.018349 | 0.025987 | 0.977920 | 00:01 |
| 20 | 0.018010 | 0.025494 | 0.978410 | 00:00 |
| 21 | 0.017696 | 0.025042 | 0.979392 | 00:00 |
| 22 | 0.017405 | 0.024627 | 0.979882 | 00:00 |
| 23 | 0.017133 | 0.024243 | 0.979882 | 00:00 |
| 24 | 0.016879 | 0.023889 | 0.979882 | 00:00 |
| 25 | 0.016640 | 0.023560 | 0.980373 | 00:00 |
| 26 | 0.016414 | 0.023254 | 0.980373 | 00:00 |
| 27 | 0.016202 | 0.022969 | 0.981354 | 00:00 |
| 28 | 0.016000 | 0.022703 | 0.981845 | 00:00 |
| 29 | 0.015809 | 0.022454 | 0.981845 | 00:00 |
| 30 | 0.015627 | 0.022222 | 0.981845 | 00:00 |
| 31 | 0.015454 | 0.022004 | 0.981845 | 00:00 |
| 32 | 0.015289 | 0.021800 | 0.982336 | 00:00 |
| 33 | 0.015132 | 0.021609 | 0.982336 | 00:00 |
| 34 | 0.014981 | 0.021429 | 0.982826 | 00:00 |
| 35 | 0.014836 | 0.021260 | 0.982826 | 00:00 |
| 36 | 0.014697 | 0.021101 | 0.982826 | 00:00 |
| 37 | 0.014564 | 0.020950 | 0.982826 | 00:00 |
| 38 | 0.014435 | 0.020808 | 0.982826 | 00:00 |
| 39 | 0.014311 | 0.020673 | 0.983317 | 00:01 |
Чтобы сэкономить место, мы не показываем здесь более 40 строк вывода. Процесс обучения записывается в learn.recorder, а таблица выходных данных хранится в атрибуте values , поэтому мы можем построить график точности обучения:
plt.plot(L(learn.recorder.values).itemgot(2));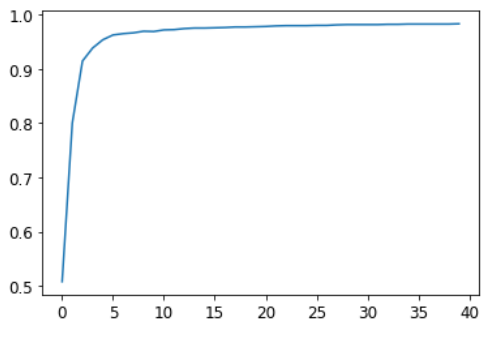
И вот, окончательная точность:
learn.recorder.values[-1][2]0.983316957950592
На данный момент у нас есть кое-что довольно волшебное:
- Функция, которая может решить любую задачу с любым уровнем точности (нейронная сеть) при правильном наборе параметров
- Способ найти лучший набор параметров для любой функции (стохастический градиентный спуск)
Вот почему глубокое обучение может делать вещи, которые кажутся довольно волшебными, такими фантастическими вещами. Вера в то, что эта комбинация простых методов действительно может решить любую проблему, - один из важнейших шагов, которые, как мы считаем, должны сделать многие студенты. Это кажется слишком хорошим, чтобы быть правдой - неужели все должно быть труднее и сложнее, чем это? Наша рекомендация: попробуйте! Мы только что опробовали это на наборе данных MNIST, и вы увидели результаты. А так как мы сами все делаем с нуля (кроме расчета градиентов), то вы знаете, что никакой особой магии за кулисами не прячется.
Идти глубже
Нет необходимости останавливаться на двух линейных слоях. Мы можем добавить столько, сколько захотим, если добавим нелинейность между каждой парой линейных слоев. Однако, как вы узнаете, чем глубже модель, тем сложнее оптимизировать параметры на практике. Позже в этой книге вы узнаете о некоторых простых, но чрезвычайно эффективных методах обучения более глубоких моделей.
Мы уже знаем, что одной нелинейности с двумя линейными слоями достаточно для аппроксимации любой функции. Так зачем нам использовать более глубокие модели? Причина в производительности. С более глубокой моделью (то есть с большим количеством слоев) нам не нужно использовать столько параметров; оказывается, что мы можем использовать меньшие матрицы с большим количеством слоев и получать лучшие результаты, чем мы получили бы с большими матрицами и несколькими слоями.
Это означает, что мы можем обучить модель быстрее, и она будет занимать меньше памяти. В 1990-х исследователи были настолько сосредоточены на универсальной аппроксимационной теореме, что очень немногие экспериментировали с более чем одной нелинейностью. Эта теоретическая, но не практическая основа сдерживала развитие этой области в течение многих лет. Некоторые исследователи, однако, экспериментировали с глубокими моделями и в конечном итоге смогли показать, что эти модели могут работать намного лучше на практике. В конце концов были получены теоретические результаты, которые показали, почему это происходит. Сегодня крайне необычно найти кого-нибудь, кто использует нейронную сеть только с одной нелинейностью.
Вот что происходит, когда мы обучаем 18-слойную модель, используя тот же подход, который мы видели в < >:
dls = ImageDataLoaders.from_folder(path)
learn = cnn_learner(dls, resnet18, pretrained=False,
loss_func=F.cross_entropy, metrics=accuracy)
learn.fit_one_cycle(1, 0.1)| epoch | train_loss | valid_loss | accuracy | time |
|---|---|---|---|---|
| 0 | 0.148737 | 0.013101 | 0.996075 | 00:19 |
Почти 100% точность! Это большая разница по сравнению с нашей простой нейронной сетью. Но, как вы узнаете в оставшейся части этой книги, есть всего несколько маленьких трюков, которые вам нужно использовать, чтобы получить такие замечательные результаты с нуля. Вы уже знаете ключевые основополагающие элементы. (Конечно, даже если вы знаете все трюки, вы почти всегда захотите работать с предварительно построенными классами, предоставленными PyTorch и fastai, потому что они избавляют вас от необходимости думать обо всех мелких деталях самостоятельно.)
Краткое изложение терминологии
Поздравляем: теперь вы знаете, как создать и обучить глубокую нейронную сеть с нуля! Мы проделали довольно много шагов, чтобы добраться до этого момента, но вы можете быть удивлены тем, насколько это на самом деле просто.
Теперь, когда мы находимся на этом этапе, это хорошая возможность определить и пересмотреть некоторые термины и ключевые концепции.
Нейронная сеть содержит множество чисел, но они бывают только двух типов: числа, которые вычисляются, и параметры, из которых вычисляются эти числа. Это дает нам два самых важных термина, которые нужно изучить:
- Активации :: Числа, которые вычисляются (как по линейным, так и по нелинейным слоям)
- Параметры :: числа, которые инициализируются случайным образом и оптимизируются (то есть числа, которые определяют модель).
В этой книге мы часто будем говорить об активациях и параметрах. Помните, что они имеют очень конкретное значение. Это числа. Это не абстрактные понятия, а реальные конкретные числа, которые есть в вашей модели. Часть того, чтобы стать хорошим практиком глубокого обучения, - это привыкнуть к идее действительно смотреть на ваши активации и параметры, строить их и проверять, правильно ли они себя ведут.
Все наши активации и параметры содержатся в тензорах . Это просто массивы правильной формы, например, матрица. Матрицы имеют строки и столбцы; мы называем их осями или размерами . Число размерностей тензора - это его ранг . Есть несколько специальных тензоров:
- Нулевой ранг: скаляр
- Первый ранг: вектор
- Второй ранг: матрица
Нейронная сеть содержит несколько слоев. Каждый слой либо линейный, либо нелинейный. Обычно мы чередуем эти два типа слоев в нейронной сети. Иногда люди называют как линейный слой, так и его последующую нелинейность вместе как один слой. Да, это сбивает с толку. Иногда нелинейность называют активационной функцией.
< > обобщает ключевые концепции, связанные с SGD. asciidoc .Deep learning vocabulary (Словарь терминов) |===== | Term (Обозначение) | Meaning (Смысл) |ReLU | Функция, которая возвращает 0 для отрицательных чисел и не меняет положительные числа. |Mini-batch (Мини-партия) | Небольшая группа входов и меток, собранных вместе в два массива. Шаг градиентного спуска обновляется для этого пакета (а не для всей эпохи). |Forward pass | Применение модели к некоторым входным данным и вычисление прогнозов. |Loss (Ошибка)| Значение, которое показывает, насколько хорошо (или плохо) работает наша модель. |Gradient ( Градиент)| Производная потерь по некоторому параметру модели. |Backward pass (Обратный проход)| Вычисление градиентов потерь по всем параметрам модели. |Gradient descent (Градиентный спуск) | Сделаем шаг в направлении, противоположном градиентам, чтобы улучшить параметры модели. |Learning rate (Скорость обучения) | Размер шага, который мы делаем при применении SGD для обновления параметров модели. |=====
Напоминание: Вы решили пропустить главы 2 и 3, чтобы заглянуть под капот? Что ж, вот вам напоминание вернуться к главе 2 прямо сейчас, потому что вам очень скоро нужно будет узнать все это!
Опросник
- Как изображение в градациях серого отображается на компьютере? Как насчет цветного изображения?
- Как структурированы файлы и папки в MNIST_SAMPLE наборе данных? Почему?
- Объясните, как работает подход «сходства пикселей» к классификации цифр.
- Что такое понимание списка? Создайте один, который выбирает нечетные числа из списка и удваивает их.
- Что такое «тензор третьего ранга»?
- В чем разница между тензорным рангом и формой? Как получить значение ранга по его форме?
- Что такое RMSE и L1 norm?
- Как вы можете применить вычисление к тысячам чисел одновременно, во много тысяч раз быстрее, чем цикл Python?
- Создайте тензор 3 × 3 или массив, содержащий числа от 1 до 9. Удвойте его. Выберите четыре цифры в правом нижнем углу.
- Что такое вещание?
- Обычно метрики рассчитываются с использованием набора для обучения или набора для проверки? Почему?
- Что такое SGD?
- Почему SGD использует мини-партии?
- Какие семь шагов в SGD для машинного обучения?
- Как мы инициализируем веса в модели?
- Что такое «потеря»?
- Почему мы не можем всегда использовать высокую скорость обучения?
- Что такое «градиент»?
- Нужно ли знать, как рассчитать градиенты самостоятельно?
- Почему мы не можем использовать точность как функцию потерь?
- Нарисуйте сигмовидную функцию. Что особенного в её форме?
- В чем разница между функцией потерь и метрикой?
- Какая функция используется для расчета новых весов с использованием скорости обучения?
- Чем занимается DataLoader класс?
- Напишите псевдокод, показывающий основные шаги, предпринятые в каждую эпоху для SGD.
- Создайте функцию, которая при передаче двух аргументов [1,2,3,4] и «abcd» возвращает [(1, «a»), (2, «b»), (3, «c»), (4, «d»)]. Что особенного в этой структуре выходных данных?
- Что делает view в PyTorch?
- Каковы параметры «смещения» в нейронной сети? Зачем они нам нужны?
- Что делает @ оператор в Python?
- Что делает метод backward ?
- Почему мы должны обнулять градиенты?
- Какую информацию мы должны передать Learner?
- Покажите Python или псевдокод для основных шагов учебного цикла..
- Что такое «ReLU»? Нарисуйте её график для значений от -2 до +2.
- Что такое «функция активации»?
- В чем разница между F.relu и nn.ReLU ?
- Универсальная аппроксимационная теорема показывает, что любую функцию можно аппроксимировать настолько точно, насколько это необходимо, используя только одну нелинейность. Так почему мы обычно используем больше?
Дальнейшие исследования
- Создайте свою собственную реализацию Learner с нуля на основе цикла обучения, показанного в этой главе.
- Выполните все шаги, описанные в этой главе, используя полные наборы данных MNIST (то есть для всех цифр, а не только для 3 и 7). Это важный проект, и на его выполнение у вас уйдет немало времени! Вам нужно будет провести собственное исследование, чтобы выяснить, как преодолеть некоторые препятствия, которые встретятся вам на пути.
Метки
Раскрыть комментарии 0
Чтобы оставить комментарий , Вам необходимо Авторизоваться или пройти Регистрацию



